PKU-Blockchain - Lecture 1

Cryptographic Hash Function

Collision resistance：抗碰撞性，现有算力无法支持人们找到 $x \neq y \Rightarrow H(x) = H(y)$。

hiding：哈希结果可以很好的隐藏明文的特征，现有算力几无法支持人们从 $H(x)$ 得到 $x$。

puzzle friendly：$z$ 作为 $H$ 的某次输出。若想找到 $c$ 使得 $H(c) = z$，是几乎不可能的。此时去寻找 $c$ 使得 $H(c) = z$ 的这一类问题变成一个 puzzle。
在区块链中，对于给定的 $target$，现需要找到一个 block header 使得 $H(block \ header) \leq target$。此时若某人完成了这个任务，那么他一定花费了很多精力（不可能是随便猜的）。 puzzle friendly 提供了工作量证明。

Bitcoin 使用的密码学哈希函数是 SHA256。

Hash Pointer

哈希指针：不光记录指前一个块的起始地址，还记录着前一个块的哈希值。

区块链就是一个使用了哈希指针来链接起来的链表。

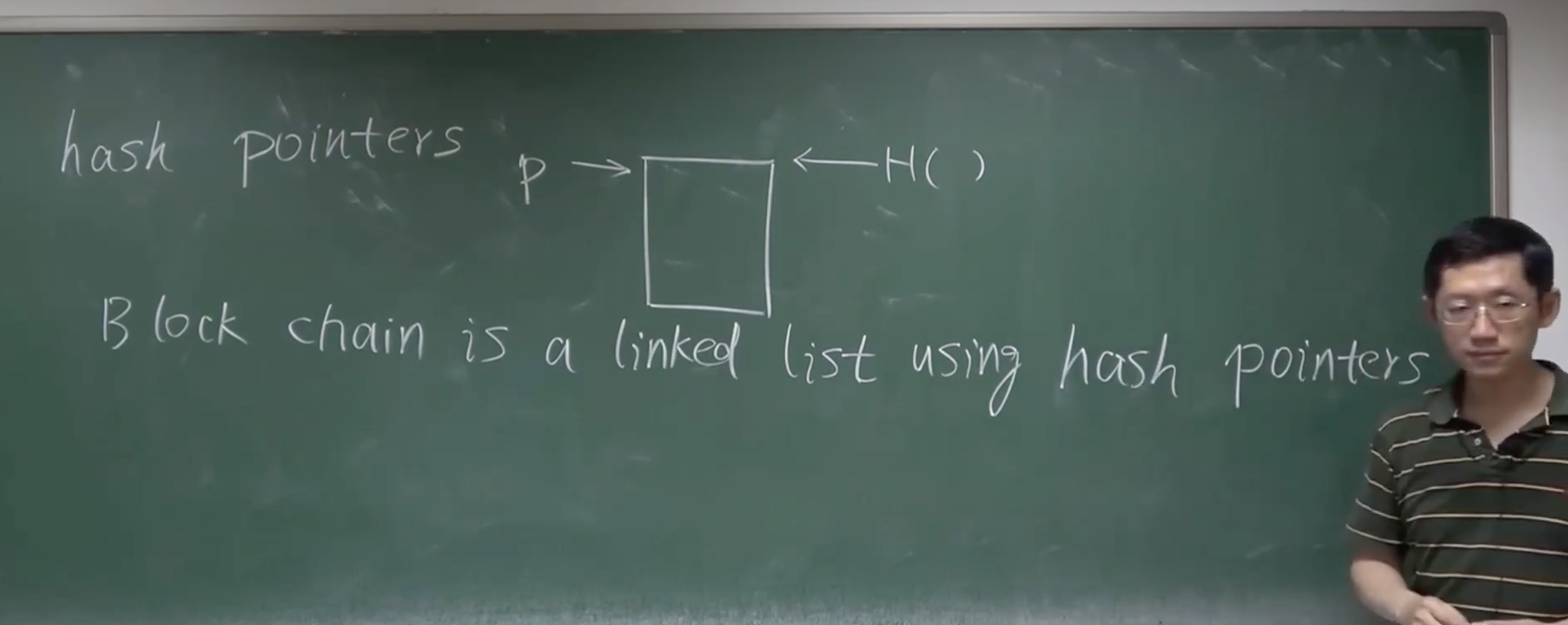
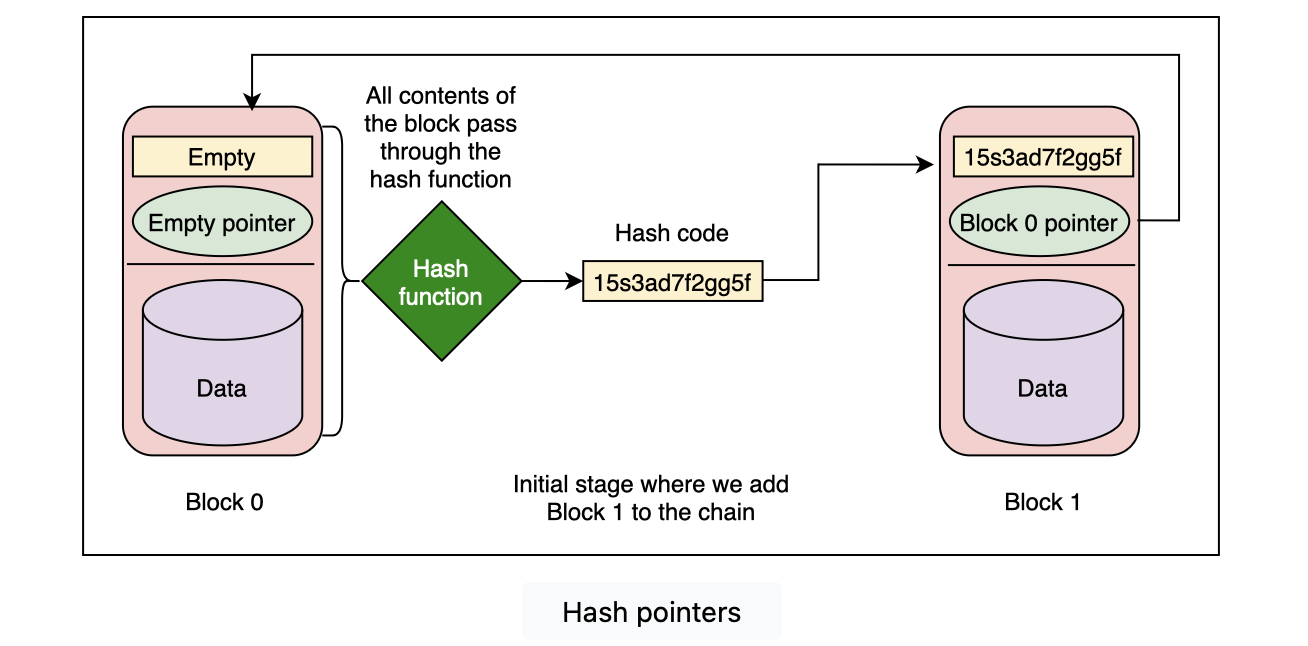
下图中不指向其他块的区块也称创世区块（genesis block）。
使用哈希指针的好处是：只需要检查最后一个块的哈希指针，即可确定前面的块中是否有被篡改的可能。实现了 tamper-evident log。

Bitcoin 用到的数据结构是 Merkle tree。

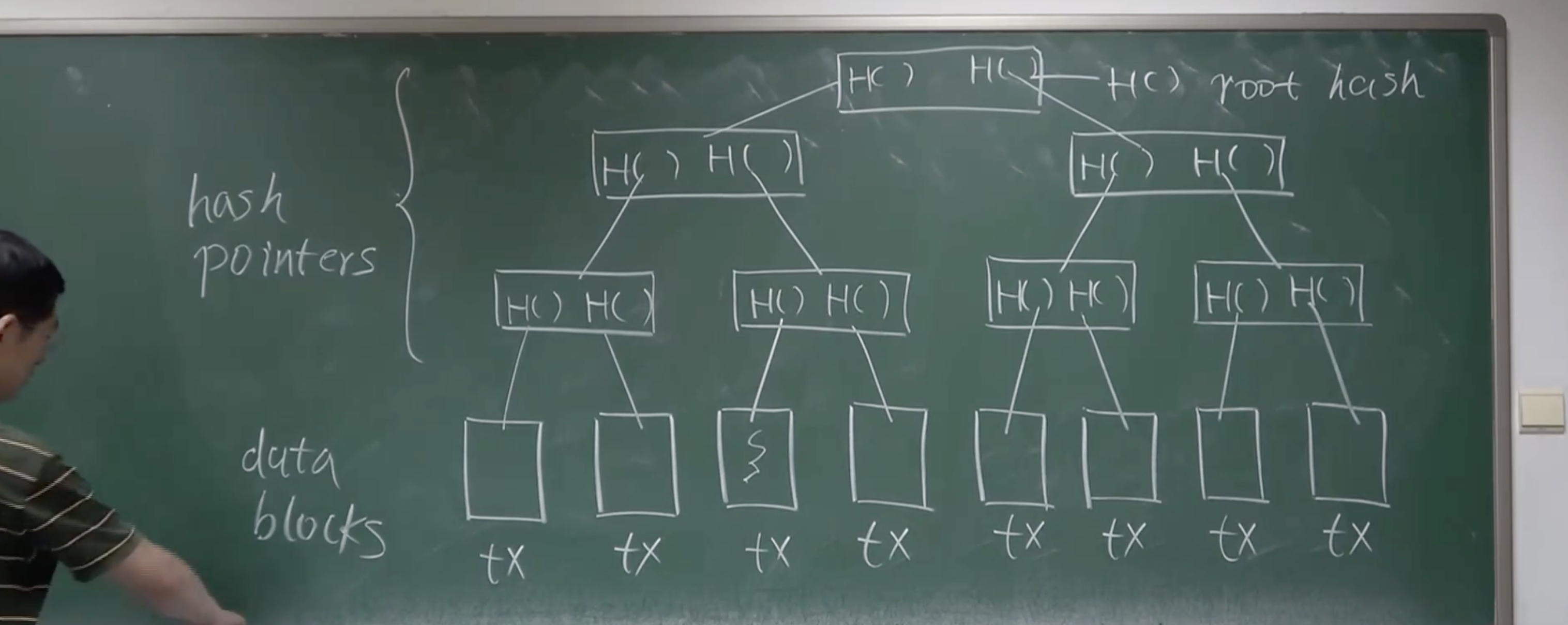
proof of membership

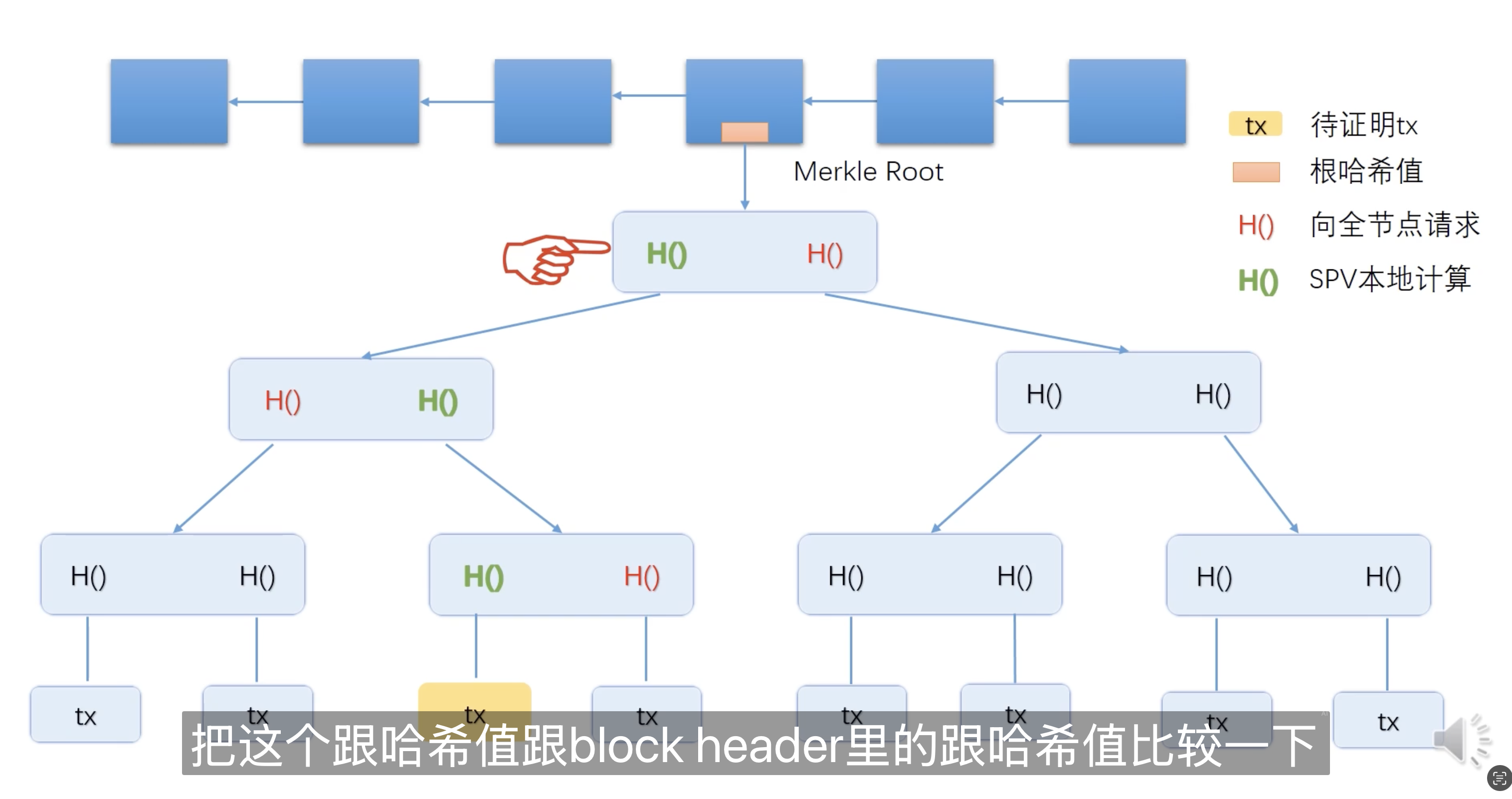
轻节点：只保留 block header，不保留 block body（具体交易的列表）
红色的Hash：全节点返回的 merkle proof
当需要验证某笔交易的真实性，只需要根据这个交易的哈希值与全节点返回的 merkle proof，向上计算，最后对比计算出来的根哈希值与自己保留的根哈希值是否相同即可。整体时间复杂度为 $O(\log n)$。

proof of nonmembership

复杂方法：将整棵树传给轻节点，让轻节点来验证整棵树的结构是否正确（对比计算出的根哈希值与自己保留的根哈希值）。整体复杂度为 $O(n)$。

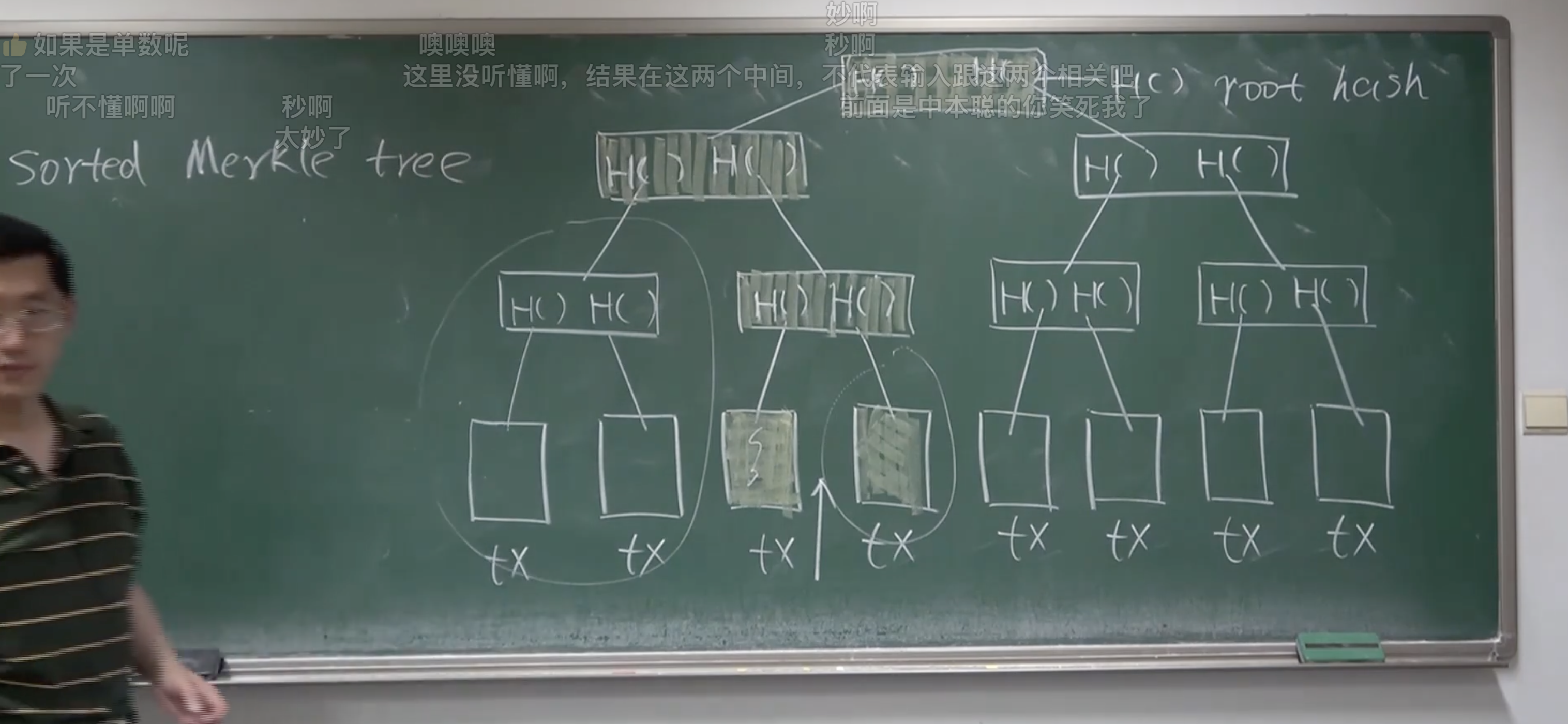
Improvement：按照哈希值进行 block 的排序（存储时就按排序后的顺序）构建 sorted merkle tree ，对想证明不存在的交易的哈希值进行二分查找。首先找不到，进而对其左右相邻的块进行验证（发给轻节点），若计算出来的根哈希值与自己保留的根哈希值相同，即可证明 nonmembership。整体复杂度为 $O(\log n)$。