1. 实验内容 模拟实现 DH 密钥交换协议(基于大素数进行算法实现),并生成会话密钥。利用会话密钥对字符串进行正确的加密和解密,且需要使得相同内容每次发送的密文不同。
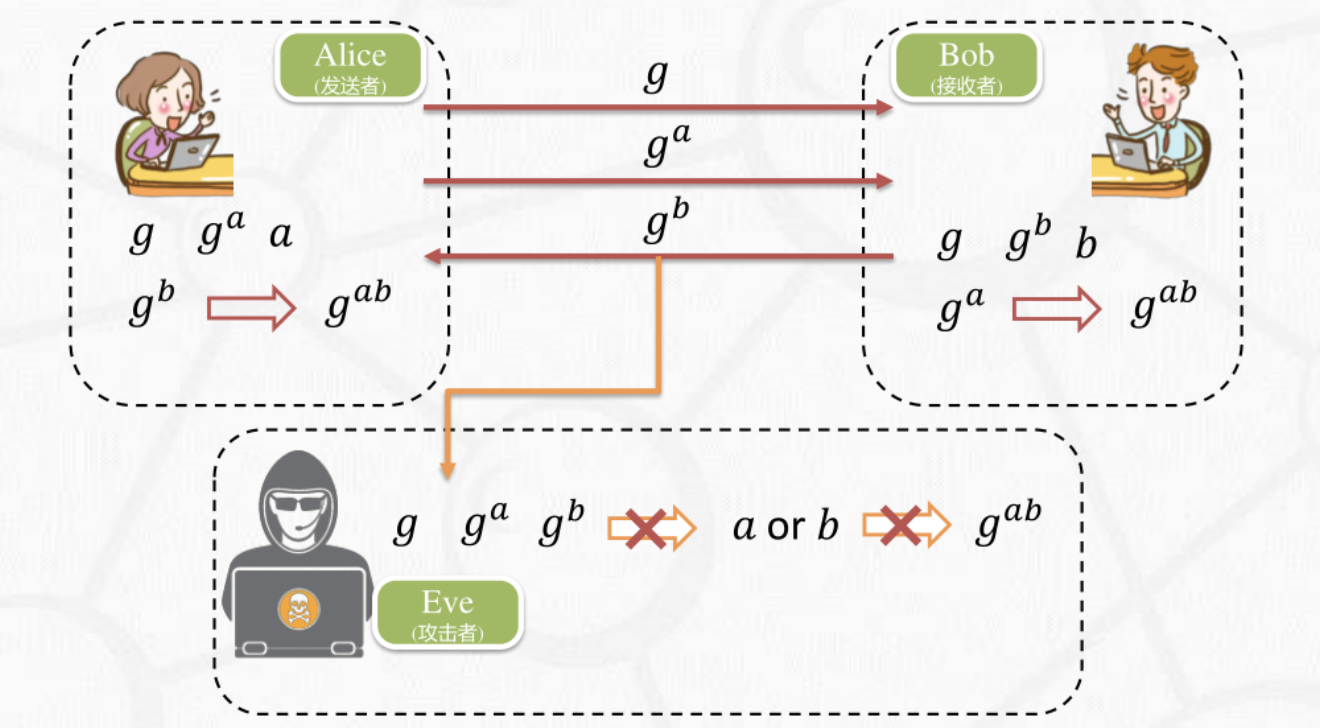
2. 实验原理 2.1 Diffie–Hellman 密钥交换协议 利用离散对数 问题的特性( $G$ 是一个单位元为 $1$ 的、其中一个生成元为 $g$ 的乘法循环群):
Alice 和 Bob 想要通过对称加密 来传输信息,现他们需要协商那个用于后续加密的密钥。
以下运算默认在模 $p$ 意义下进行。
在整个过程中,$g$, $g ^ a$, $g ^ b$, $p$ 都作为公开信息在信道上传输,有被 Eve 获取到的可能性。但很难从这些信息推出 $a$ 与 $b$。$g ^ {ab}$ 就作为那个协商好的密钥。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def generate_large_prime (bits ): while True : candidate = random.getrandbits(bits) prime_candidate = nextprime(candidate) if prime_candidate.bit_length() == bits: return prime_candidate g = generate_large_prime(1024 ) p = generate_large_prime(1024 ) print ("\nThe 1st 1024-bit big prime number is: " , g)print ("\nThe 2nd 1024-bit big prime number is: " , p)a = randint(2 **10 , 2 **20 ) b = randint(2 **10 , 2 **20 ) x = pow (g, a, p) y = pow (g, b, p) keya = pow (y, a, p) keyb = pow (x, b, p) print ("\nA's secret key is:" , keya)print ("\nB's secret key is:" , keyb)if keya == keyb : print ("\nA's secret key is equal to B's secret key." ) print ("\nDiffie-Hellman key exchange succeed." )
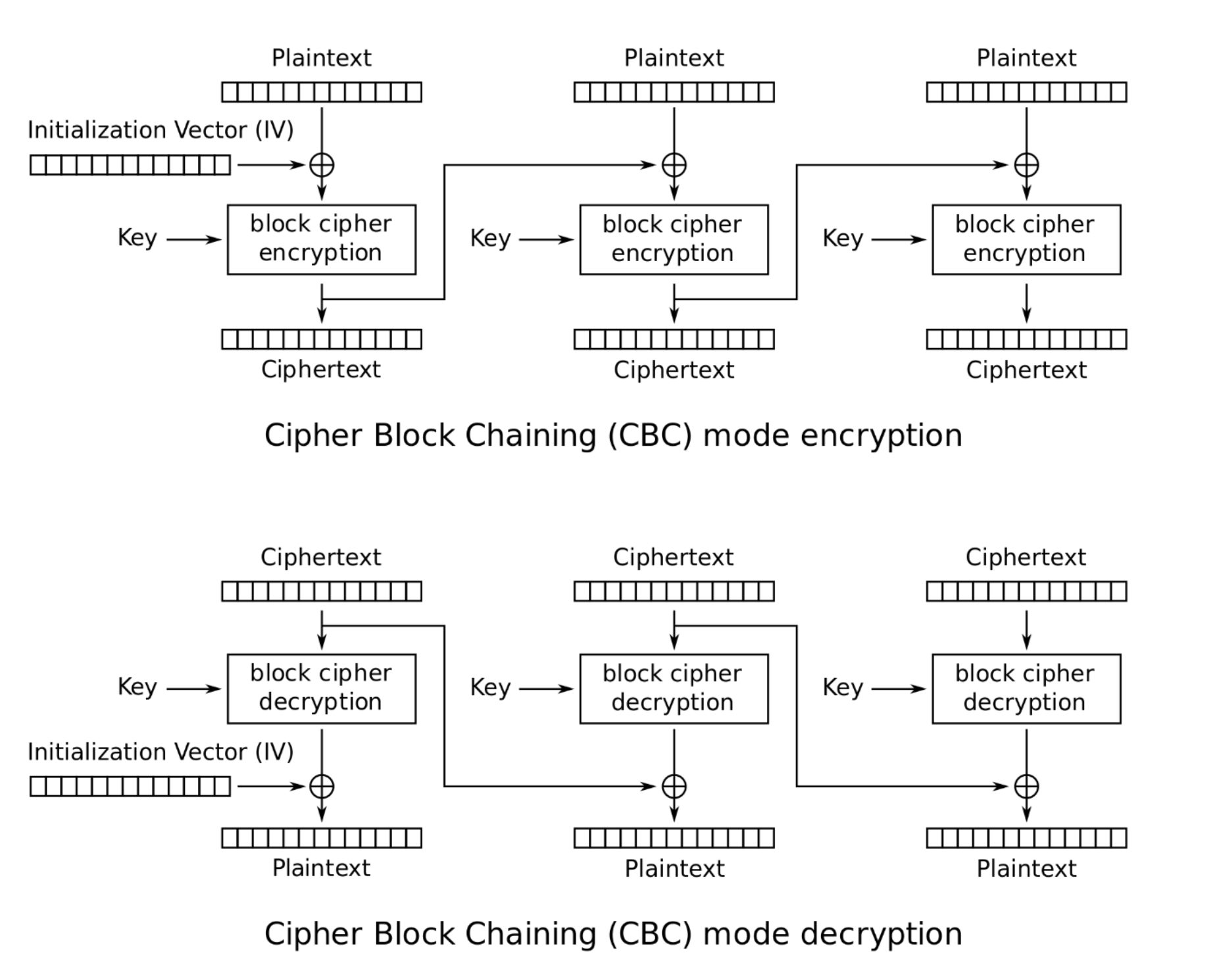
2.2 AES 加解密 AES 加密算法在该实验中通过 Crypto.Cipher.AES 模块实现,具体使用的是 CBC(Cipher Block
AES 是一种分组加密算法,它将明文分成固定大小的块,然后使用相同的密钥 对每个块进行加密。本次实验中 AES 密钥的长度为 256 位(使用 SHA256 方法),分组块的长度为 128 位。
CBC 模式通过将前一个密文块的加密结果(除了第一个块,使用初始化向量IV)与当前明文块进行异或操作后再加密,从而增加加密的复杂性和安全性。这种模式可以有效防止相同明文块产生相同的密文块,提高了安全性。
代码中还引入了 pad 与 unpad 功能。使用他们是为了确保 AES 加密和解密操作的正确性和完整性(AES 算法要求加密的数据必须是固定大小的块)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def generate_key (secret ): key = hashlib.sha256(secret.encode()).digest() return key def encrypt_message (message, key ): cipher = AES.new(key, AES.MODE_CBC) ciphertext = cipher.encrypt(pad(message.encode(), AES.block_size)) iv = cipher.iv return iv + ciphertext def decrypt_message (encrypted_message, key ): iv = encrypted_message[:AES.block_size] ciphertext = encrypted_message[AES.block_size:] cipher = AES.new(key, AES.MODE_CBC, iv) decrypted_message = unpad(cipher.decrypt(ciphertext), AES.block_size) return decrypted_message.decode()
3. 实验结果
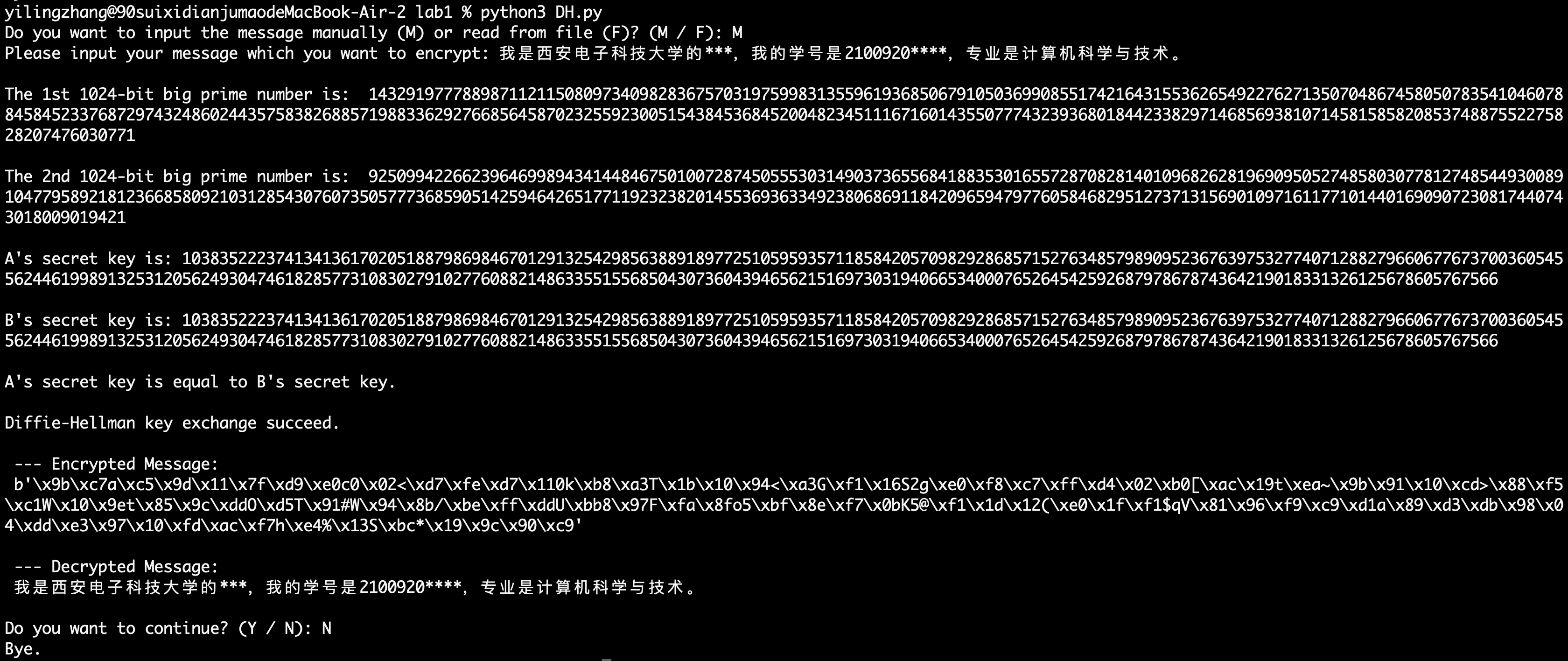
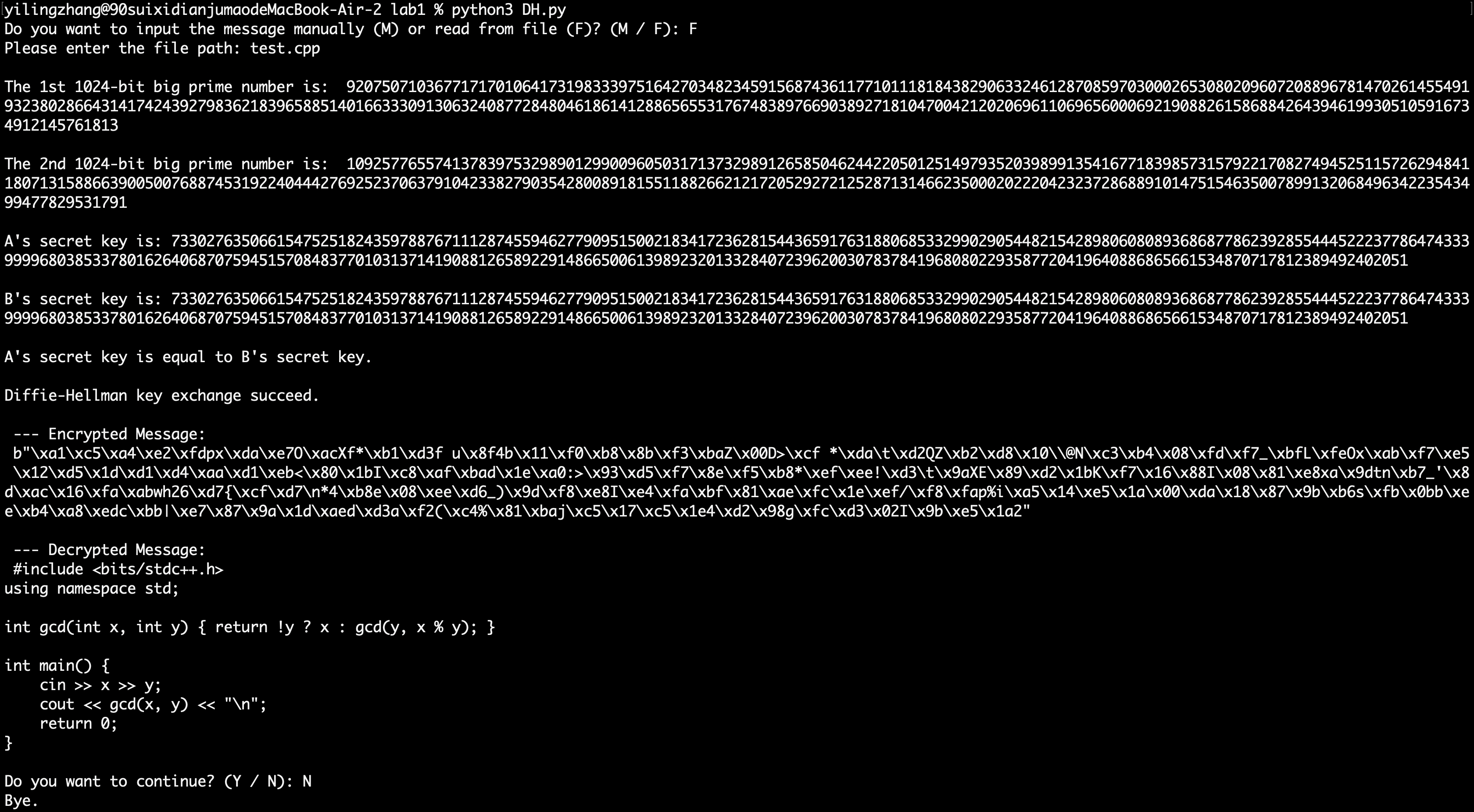
上面两个结果表明,可以选择命令行手动输入/本地文件输入想要加密的信息。程序成功生成了两个大素数,且在此基础上计算出来的 Alice 与 Bob 的密钥(共享密钥)相同,说明成功共享了一个用于后续加密的密钥。
后续给出了 AES 的加密结果、解密结果,解密结果与输入的内容一致。
4. 实验心得 Python 中提供了很方便的库,让复杂的加密过程得以被轻松的实现。
本人只实现了对文本文件的加解密,可以提升的地方包括:支持其他文件类型的加解密(如图片、pdf等)、支持将加密结果无差错的保存至本地的文件中。