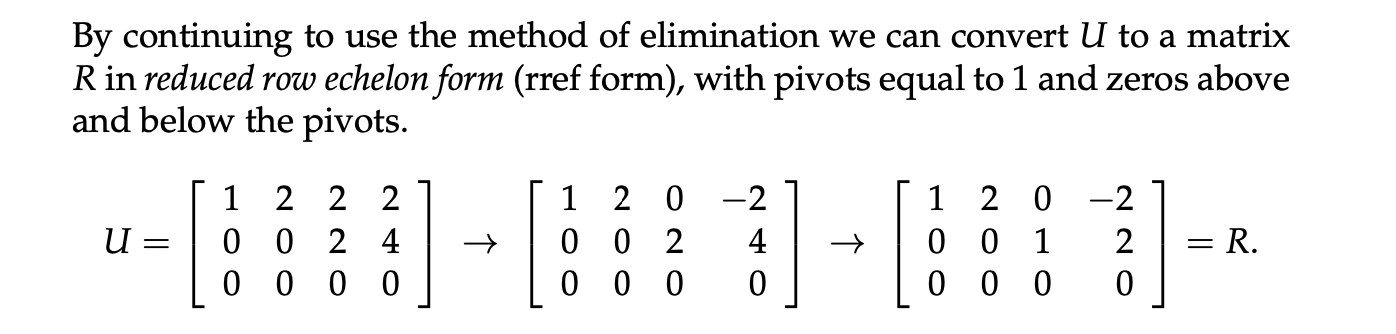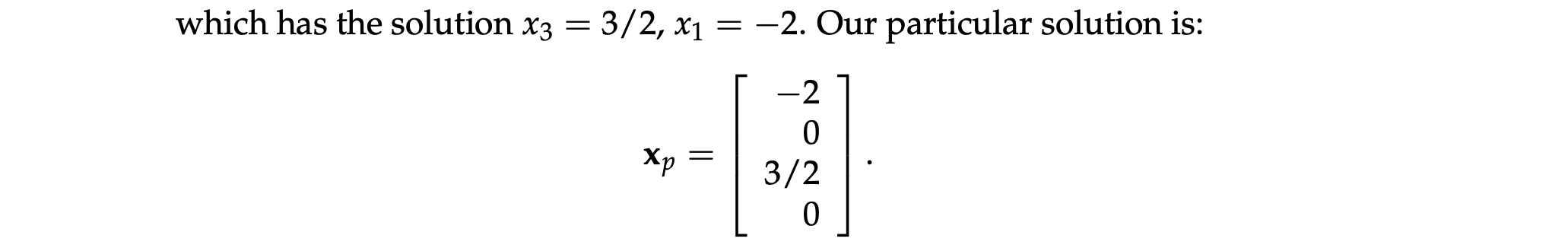MIT 18.06 - Lecture 7 & 8

Solving Ax = 0

对 $A$ 进行消元。
在消元的过程中，可能会遇见该列没有主元的情况，继续寻找下一个主元即可。
在消元的过程中，可能会遇见某一行被消为 0 的情况：这说明在 $A$ 中这一行是其他行的线性组合。

有主元的列（pivot columns），没主元的列（free columns）对应的方程组中的变量 $x_2, x_4$ 可以取任意值，也称他们为自由变量。通过自由变量的取值，可以确定主元的取值。

矩阵中主元的个数 $r$ 也被称作该矩阵的秩（rank），自由变量的个数 $m = n - r$。一般每个自由变量轮流取值为 $1$，其余全都取 $0$。由此可以得到 $m$ 个特解。这 $m$ 个特解的线性组合就是 $A$ 对应的零空间。

通过消元，使得 $Ax = 0$ 变成 $Ux = 0$；再将所有 pivots 的值都变成 1，且 pivots 之上和之下都变成 0，实现从 $Ux = 0$ 变成 $Rx = 0$ 的过程。

最终的 $R$ 被称作简化行阶梯形式（reduced row echelon form）的矩阵。

由于 $A$ 对应的零空间是 $A$ 中列向量的线性组合，所以可以将 $A$ 的列进行交换。
转化成上图中 $R$ 的形式后，可以借助矩阵乘法，引入一个零空间矩阵 $N$ 使得 $RN = 0$，不难得出 $N$ 的样子。

$N$ 中的每一列就是自由变量不同取值所得到的特解，$N$ 中列向量线性组合的结果就是 $N$ 所对应的零空间。用这种方法可以很快的得到 $Ax = 0$ 的解。

Solving Ax = b

“If there is a solution $x$ to $Ax = b$, then $b$ must be a linear combination of the columns of $A$. The system of linear equations $Ax = b$ is solvable exactly when $b$ is a vector in the column space of A.”

满足条件 $Ax = b$ 的所有解：特解 + 零向量空间中的所有向量。

特解：让所有的自由变量取值为 0。

Augmented matrix：增广矩阵

由于 $Ax_p = b , \ Ax_n = 0 \Rightarrow (Ax_p + Ax_n = b, \ A(x_p + x_n) = b)$，故通过这种方式可以得到所有满足条件的解。

上图中的 $x_{complete} = \cdots$ 中，第二项前少加了 $c_1$。

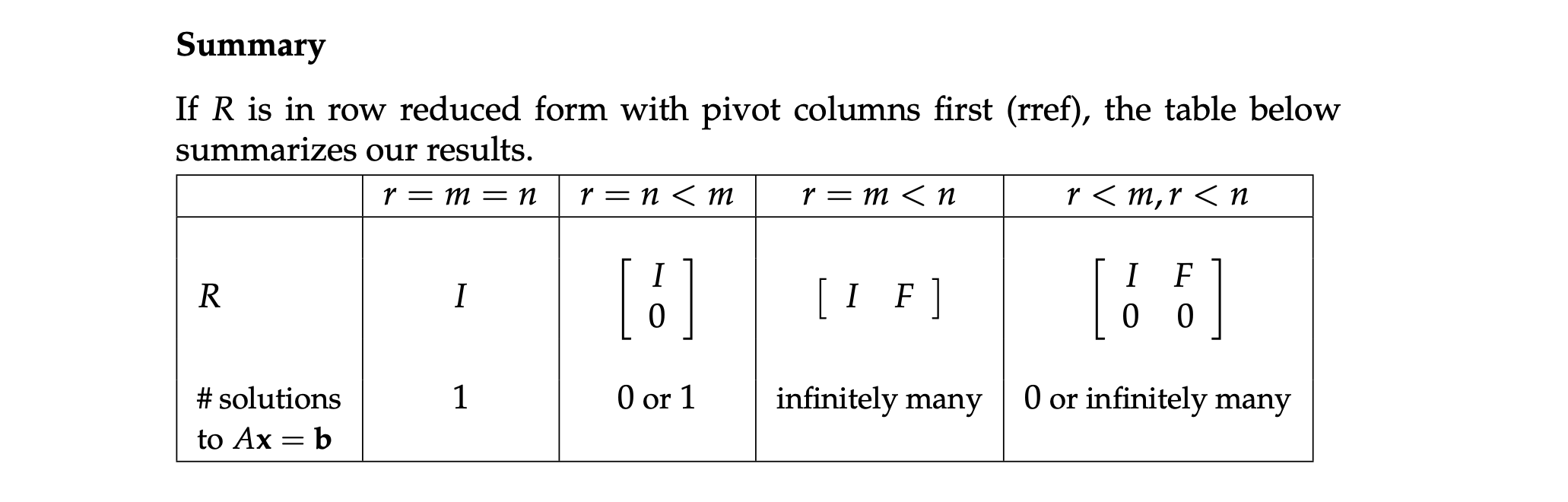
矩阵的秩与线性方程组的解的关系

对于一个 $m \times n$ 的矩阵 $A$，其秩为 $r$。

行满秩（Full row rank, r = m）

最简矩阵形式：$ \left[\begin{array}{c}
I \quad F
\end{array}\right]$
没有全是 $0$ 的行，故对 $b$ 无要求（因为消元后不会出现 $0 = b$ 的线性组合 的情况），即 $Ax = b$ 对任何 $b$ 始终有解，且有无穷多解。
自由变量的个数 $= n - r = n - m$（零空间的维度是 $n - m$）。

列满秩（Full Column rank, r = n）

最简矩阵形式：$ \left[\begin{array}{c}
I \
0
\end{array}\right]$

在这种情况下，零向量空间只包含零向量，也代表着列向量们是线性无关的。

自由变量的个数 $= n - r = n - n = 0$（自由变量的个数相当于是零空间的维度），即若 $Ax = b$ 有解，则必定是唯一解。即在列满秩的情况下，$Ax = b$ 的解的个数是 0 或 1。

行列同时满秩（Full row and column rank, r = m = n）

最简矩阵形式：$I$
代表着 $A$ 是一个可逆方阵。
The nullspace has dimension zero, and $Ax = b$ has a unique solution for every $b$ in $R ^ m$.