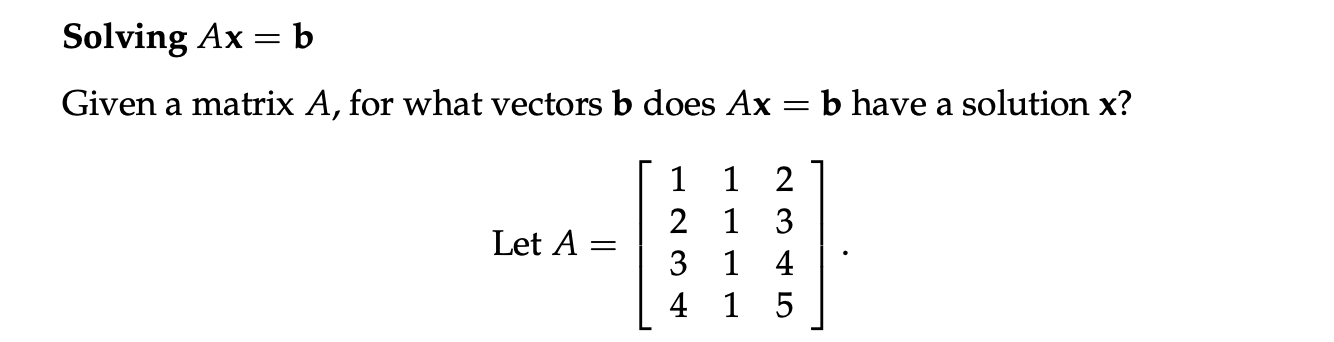MIT 18.06 - Lecture 5 & 6

置换矩阵（permutation）

$$
P ^ {-1} = P ^ T \ P P ^ {-1} = I
$$

转置（transposes）

$$
(A ^ T){ij} = A{ji}
$$

对称矩阵（symmetric martix）

满足 $A ^ T = A$ 的矩阵，称为对称矩阵。
构造对称矩阵的通用方法：$\forall A$（所有矩阵，不是方阵也可以），$A ^ TA$ 一定是一个对称矩阵。（$(A ^ TA) ^ T = A ^ TA$）。

向量空间（vector spaces）

If a collection of vectors is closed under linear combinations (i.e. under addition and multiplication by any real numbers), and if multiplication and addition behave in a reasonable way , then we call that collection a vector space.

向量子空间（vector subspaces）

A vector space that is contained inside of another vector space is called a subspace of that space.

The union $P \cup L$ of those two subspaces is not a subspace, the intersection $S \cap T$ of those two subspaces is a subspace.

向量列空间（column spaces）

If there is a solution $x$ to $Ax = b$, then $b$ must be a linear combination of the columns of $A$. The system of linear equations $Ax = b$ is solvable exactly when $b$ is a vector in the column space of A.

向量零空间（nullspace）

使得 $Ax = 0$ 的 $x$ 组成了矩阵 $A$ 的向量零空间（为什么是空间的证明很简单，在上面已给出）。
但使得 $Ax = b, b \neq 0$ 的 $x$ 构不成一个空间，因为不包含零向量。