UCB - CS161 - Lecture 5
1. Kerckhoff’s Principle
Cryptosystems should remain secure even when the attacker knows all internal details of the system.
The key should be the only thing that must be kept secret, and the system should be designed to make it easy to change keys that are leaked (or suspected to be leaked).
If your secrets are leaked, it is usually a lot easier to change the key than to replace every instance of the running software.
加解密算法是公开的,加解密密钥是保密的:
维护密钥的保密性更容易。
若密钥暴露,换密钥即可。
面对多对加密通信的需求,使用相同的加密算法和不同的密钥即可。相比于使用不同的加密算法,设计成本和复杂程度及各方面代价都大大降低。
开放密码学设计的优势:
可以使该算法承受公开的钻研和分析,因此可以变得更加强壮。
公开后有更大的可能被正义黑客发现,比被敌人发现要好。
公开设计使标准更容易建立。
系统的安全取决于算法的保密性,对代码的逆向抵抗力很差。密钥不是代码的一部分,不存在这个问题。
2. Symmetric-Key Encryption
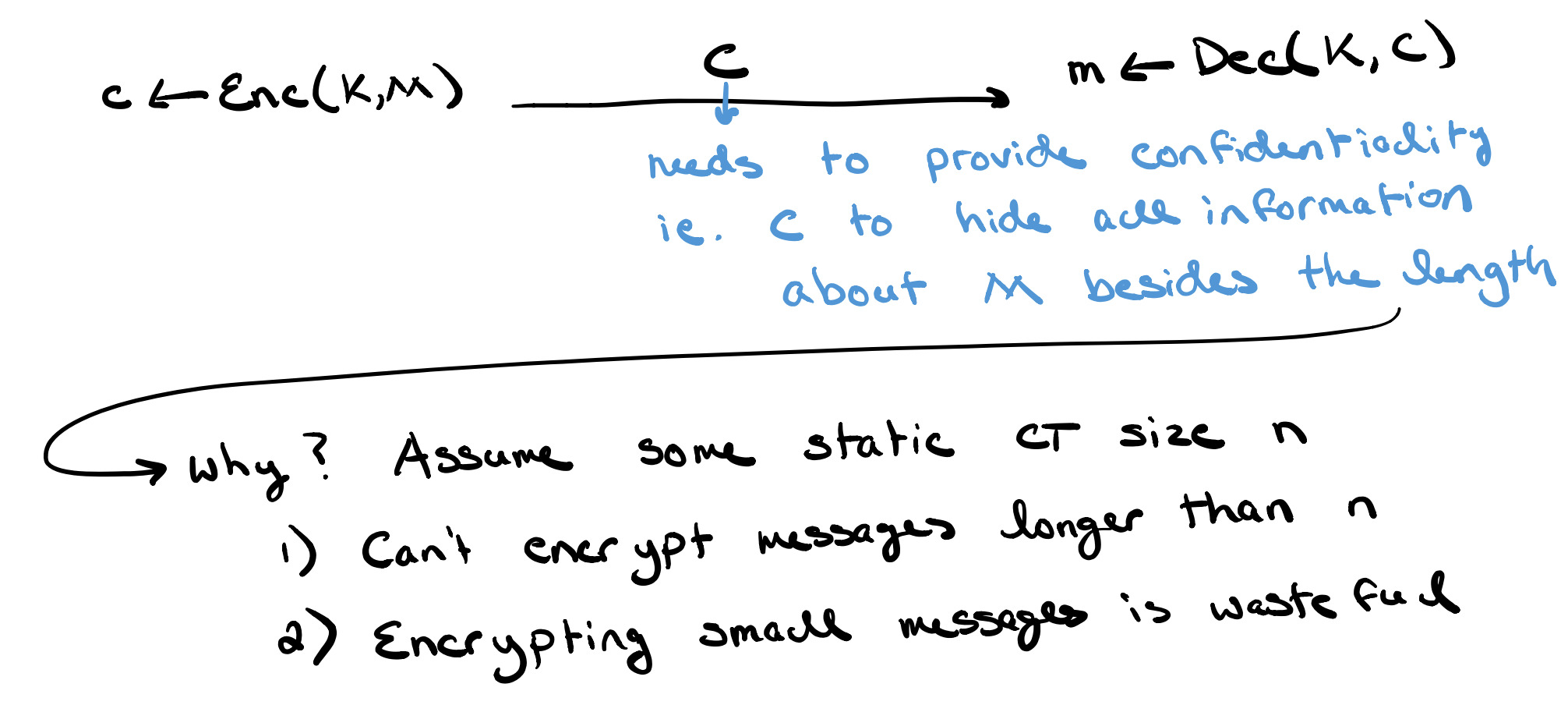
密文的长度无需成为加密的信息(从反面的角度来论证这种做法的优势)。
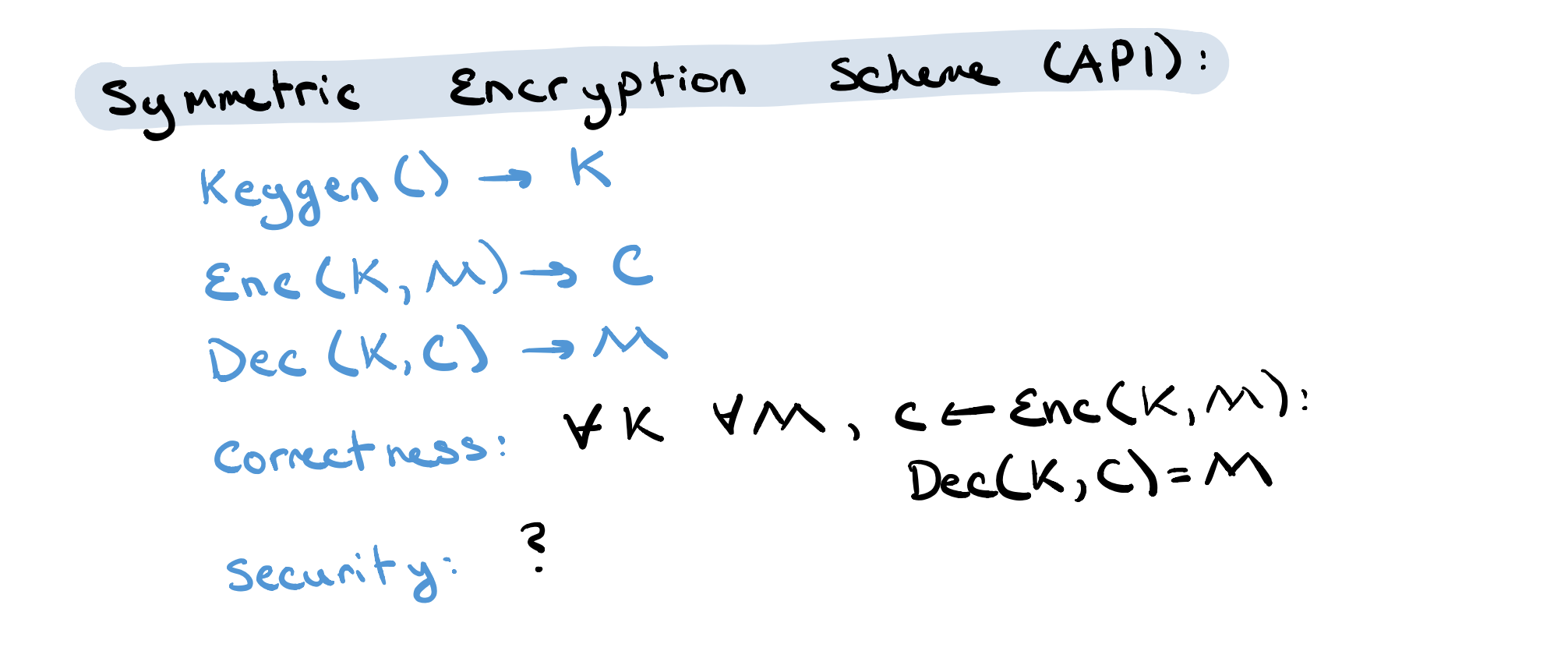
对称加密的大体模式:
安全性的考量:
partial information leak(通过加密程序返回的密文试探有关信息)
deterministic encryptions(相同明文的密文一旦相同,被破解后能大大加快破解全部密文的速度)
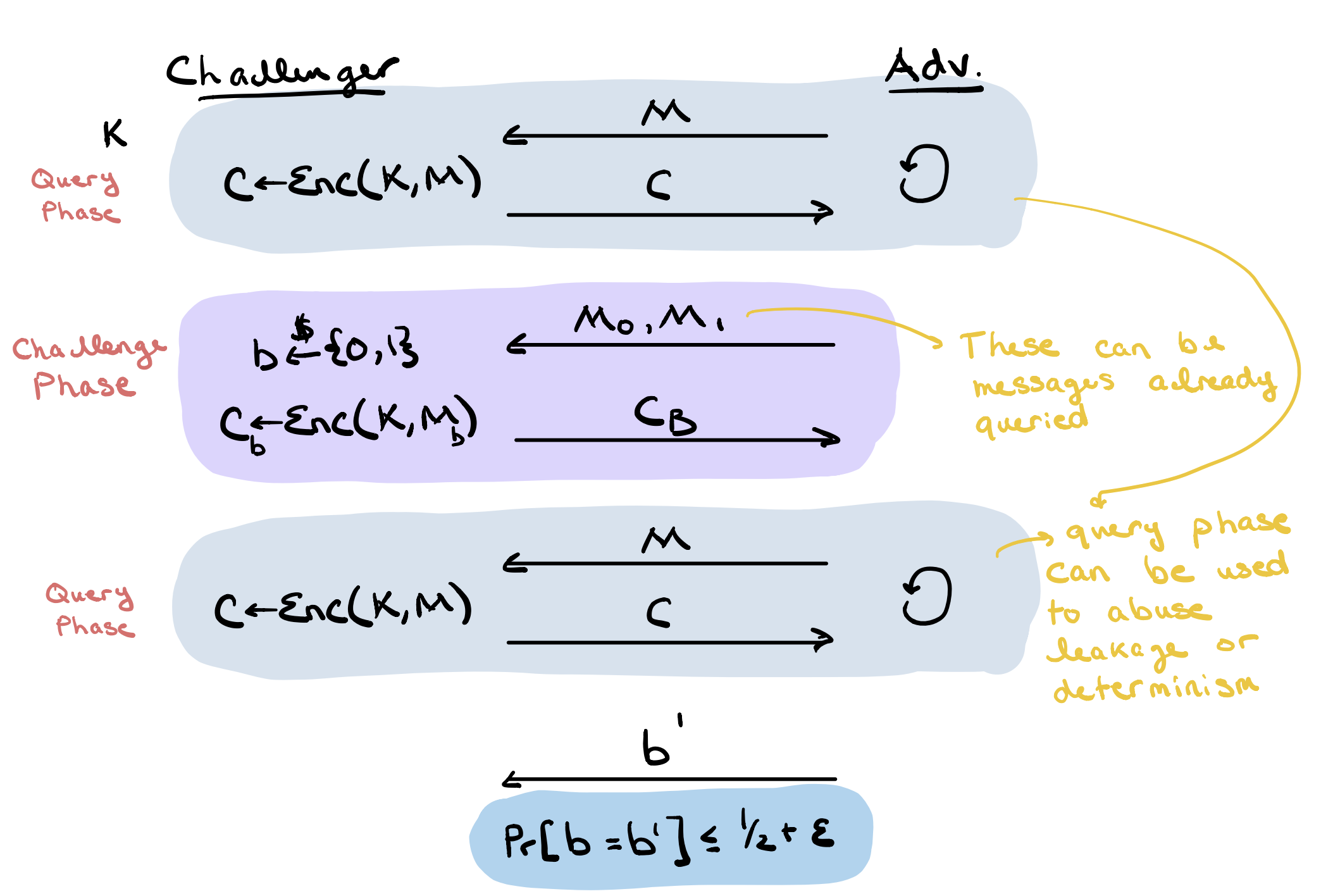
2.1 IND-CPA Security
IND-CPA:Indistinguishability under Chosen-plaintext Attack(选择明文攻击下的不可区分性)。
2.2 One-Time Pad
虽安全性极高,但只能用于一次性加密解密,不符合 IND-CPA。
Both the size of key $K$ and message $M$ is $n$,$K = k_1k_2 \cdots k_n$(randomly chosen), $C = Enc(K, M) = K \oplus M$,$Dec(K, C) = K \oplus C = K \oplus K \oplus M = M$。
2.3 Block Ciphers
Intuitively, a block cipher transforms a fixed-length, $n$-bit input into a fixed-length $n$-bit output. The block cipher has $2 ^ k$ different settings for scrambling, so it also takes in a $k$-bit key as input to determine which scrambling setting should be used.
Encryption function $E:{0, 1} ^ k \times { 0, 1} ^ n \rightarrow { 0, 1} ^ n$,This notation means we are mapping a $k$-bit input (the key) and an $n$-bit input (the plaintext message) to an $n$-bit output (the ciphertext).
Once we fix the key $K$, we get a function mapping $n$ bits to $n$ bits:$E_k : { 0, 1} ^ n \rightarrow { 0, 1} ^ n$.
The inverse mapping of this permutation is the decryption algorithm $D_k$:$D_k(E_k(M)) = M$.
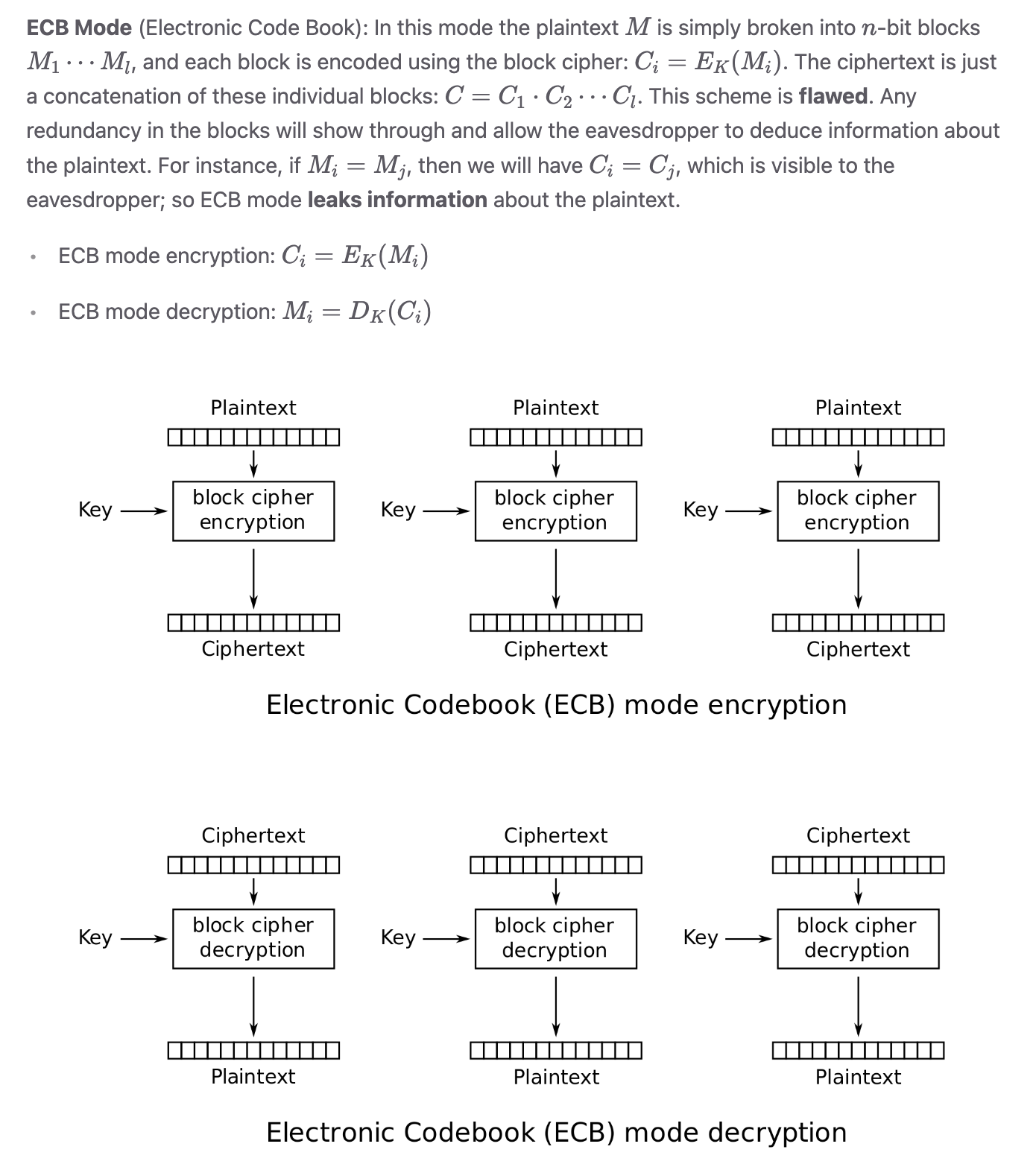
2.3.1 ECB Mode
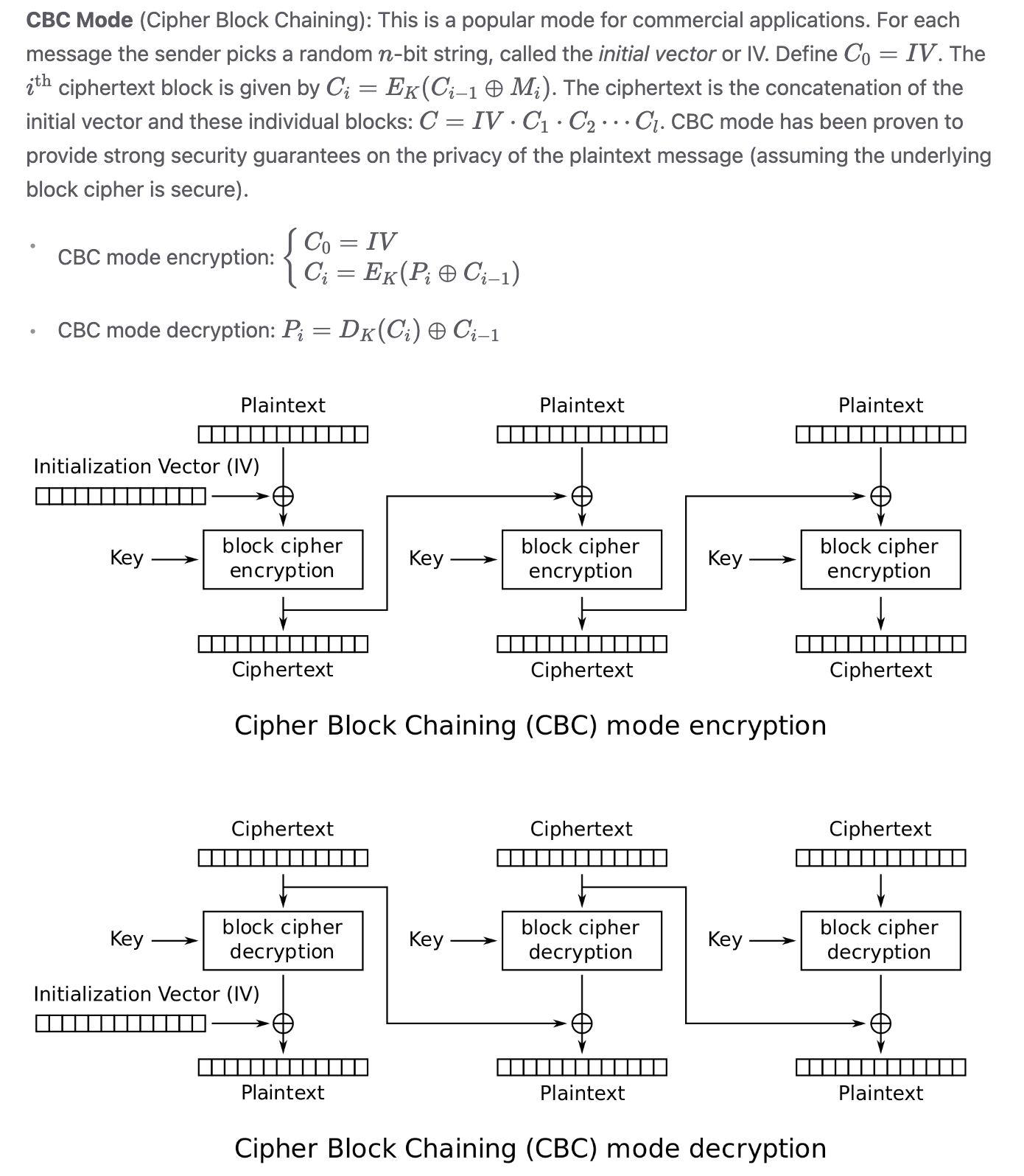
2.3.2 CBC Mode
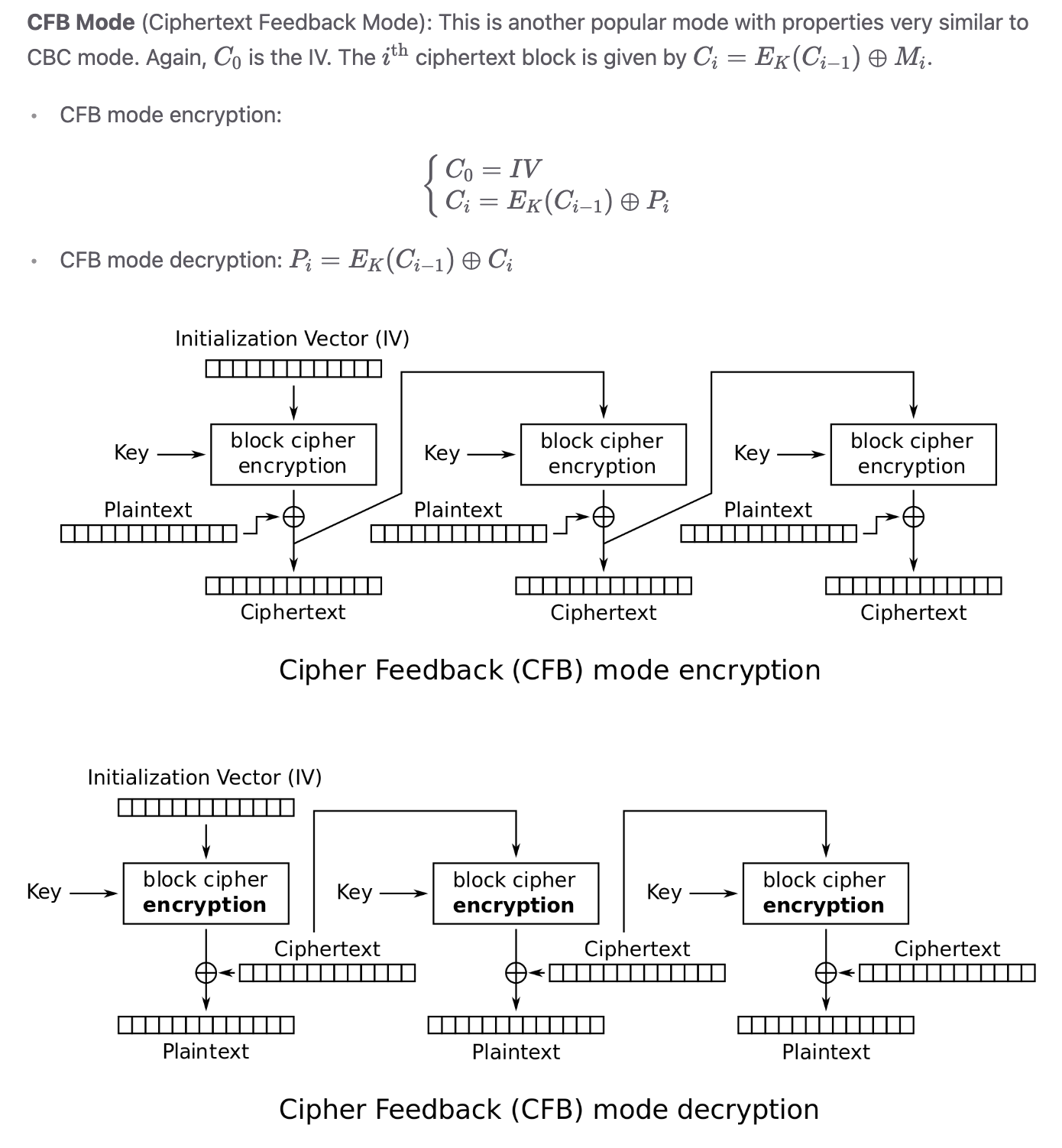
2.3.3 CFB Mode
UCB - CS161 - Lecture 5