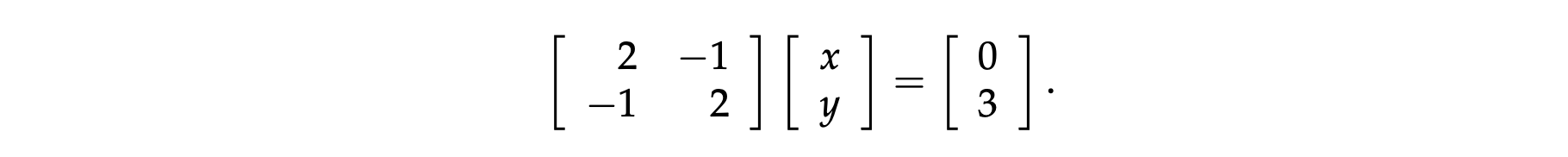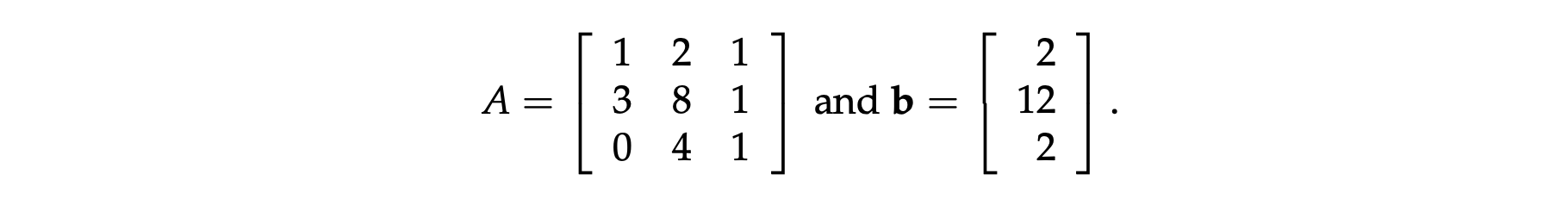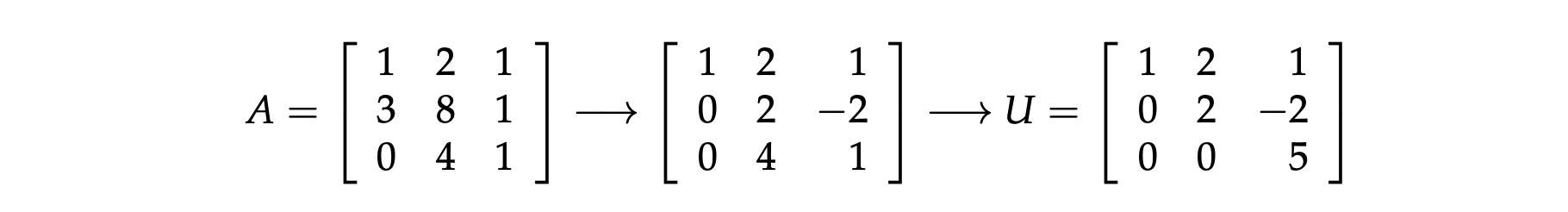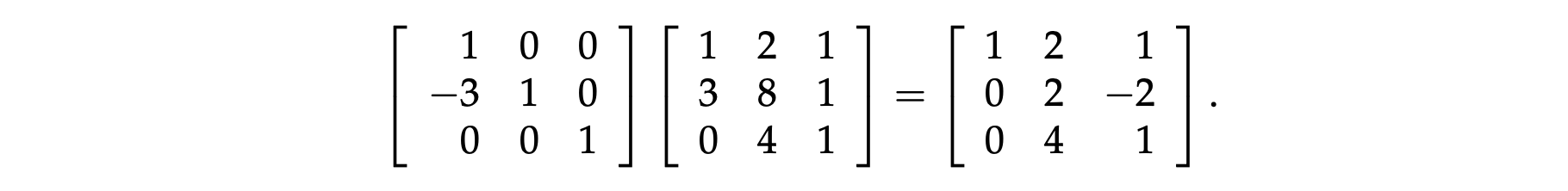MIT 18.06 - Lecture 1 & 2
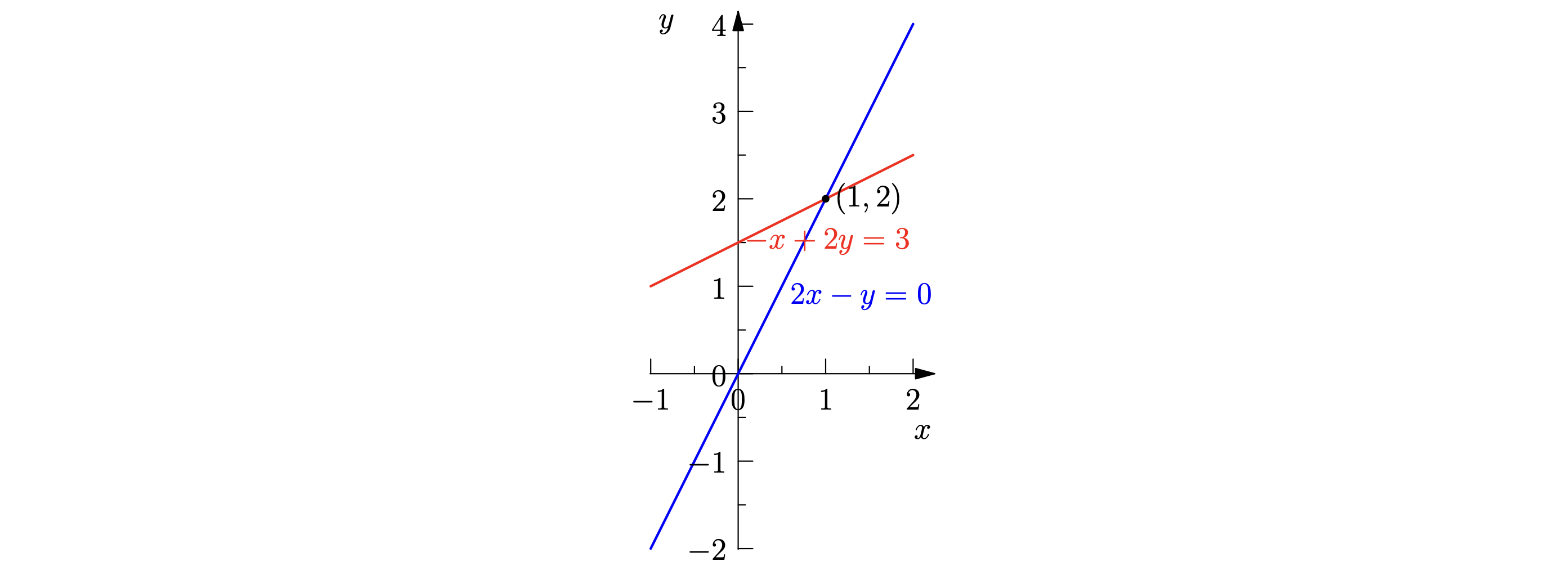
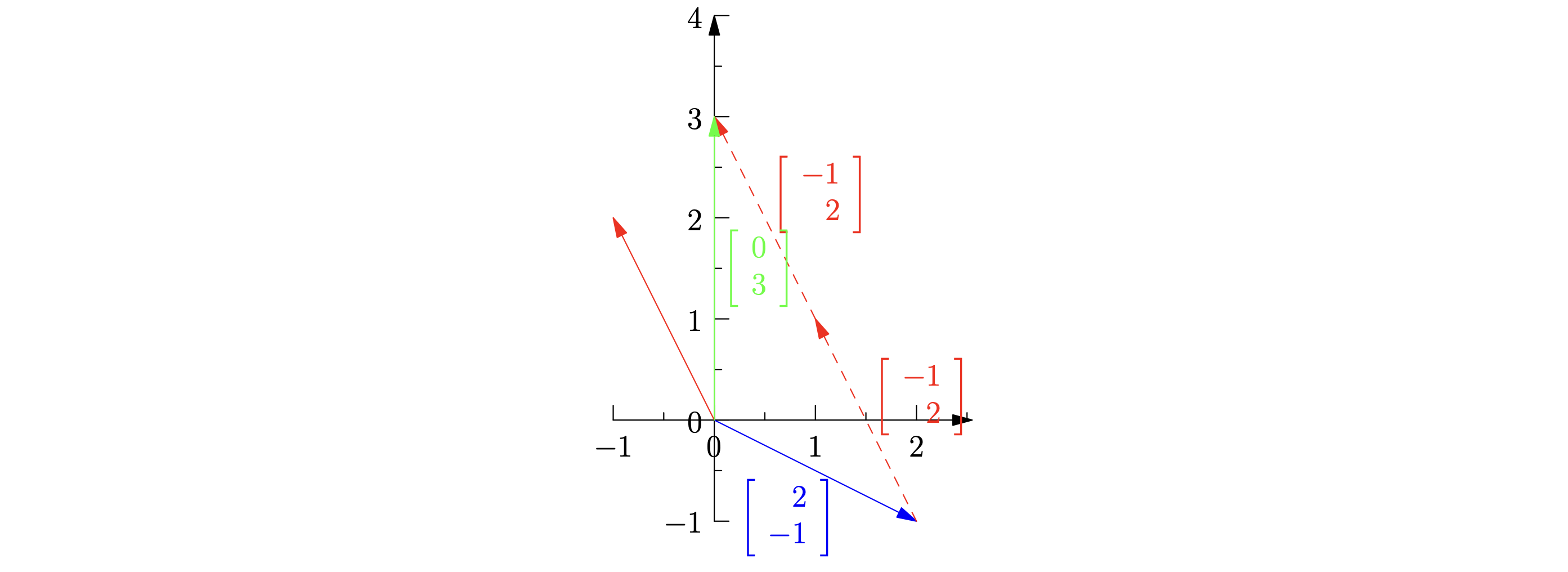
线性方程组的几何化
e.g.
$$
2x - y = 0 \
-x + 2y = 3
$$
行视角（Row Picture）:解集是直线们的交点 或 平面们的交线等。
列视角（Column Picture）:找到已知向量组的线性组合，来表达出目的向量。
矩阵视角（Matrix Picture）:写成 $Ax = b$ 的形式，其中 $A$ 是系数矩阵，$x$ 是未知数向量，$b$ 是结果向量。
线性（不）相关
给定矩阵 $A$ ，若对于任意一个向量 $b$ ，都能找到一个向量 $x$ 满足 $Ax = b$，则说明$A$ 中的列向量们的线性组合”可以触碰到所处空间的任何一个角落”（二维平面、三维空间……），称 $A$ 中的列向量们是线性不相关的（linearly independent）。
若不能，则称 $A$ 为奇异矩阵（singular matrix），在这个奇异矩阵中的列向量们是线性相关的（linearly dependent），因此他们的线性组合总是汇集在一个点/一条线/一个平面/…上，因此无法触碰到所处空间的任何一个角落。
高斯消元法 (Guass Elimination)
求解线性方程组的解时，若采用矩阵视角，可以写成 $Ax = b$。
e.g.
然后通过消元，求解出未知数向量 $x$ 即可（保证 $A$ 可逆），步骤如下：
找到该行的
pivot，将下面每行该位置的数变成 0（**We recopy the first row, then multiply the numbers in it by an appropriate value and subtract those values from the numbers in the second row.**）。若该行的
pivot为 0 ，可以通过把后续行与该行进行交换，来继续消元。直到 $A$ 变成一个上三角矩阵 $U$（upper triangular matrix），停止消元。
通过上述步骤，我们把 $Ax = b$ 变成了 $Ux = c$ 的形式，接着通过回代法（back substitution）便可以得到原方程的解。
$$
\quad
$$
刚才 $A$ 变成 $U$ 的过程，可以用矩阵乘法来描述。每次消元的步骤 1，都可以表示成在当前矩阵的左侧乘上了一个消元矩阵（下图左侧的消元矩阵叫做 $E_{21}$，因为我们正在想办法将矩阵中第 2 行第 1 列的数字消去）。
所以上述例子的 $A$ 到 $U$ 的过程，可以描述为 $E_{32}(E_{31}(E_{21}A)) = U$，也可以写成:
$$
(E_{32}E_{31}E_{21})A = U \
EA = U, \ E = E_{32}E_{31}E_{21}
$$
$$
\quad
$$
还可以发现一些有趣的性质：
- 若想对 $A$ 进行行变换，则在 $A$ 左边乘上对应的行变换矩阵。
$$
\left[\begin{array}{c}
0 & 1 \
1 & 0
\end{array}\right]
\left[\begin{array}{c}
a & b \
c & d
\end{array}\right] =
\left[\begin{array}{c}
c & d \
a & b
\end{array}\right]
$$ - 若想对 $A$ 进行列变换，则在 $A$ 右边乘上对应的列变换矩阵。
$$
\left[\begin{array}{c}
a & b \
c & d
\end{array}\right]
\left[\begin{array}{c}
0 & 1 \
1 & 0
\end{array}\right] =
\left[\begin{array}{c}
b & a \
d & c
\end{array}\right]
$$
是矩阵乘法中行变换、列变换的基础。
MIT 18.06 - Lecture 1 & 2