发表更新专业知识19 分钟读完 (大约2809个字)

算法分析与设计 - Lab2 - 排序算法的性能比较

一. 实验目的

实现插入排序（Insertion Sort，IS），自顶向下归并排序（Top-down Mergesort，TDM），自底向上归并排序（Bottom-up Mergesort，BUM），随机快速排序（Random Quicksort，RQ），Dijkstra 3-路划分快速排序（Quicksort with Dijkstra 3-way Partition，QD3P）。

二. 实验内容

在计算机上针对不同输入规模数据进行实验，对比上述排序算法的时间及空间占用性能。要求对于每次输入运行 10 次，记录每次时间/空间占用，取平均值。

三. 实验过程

首先需要明白实验中所需排序算法的基本原理。笔者在相同的实验环境下分别实现了这几种排序，尽量保证了实验结果不受环境所影响。

1. 插入排序（Insertion Sort，IS）

该排序每次将一个元素放到序列中的正确位置，做法是与它前面的元素依次比较，直到找到正确的位置。

正确性证明显而易见：由于是从左往右依次处理每个位置的元素的，所以待排元素左边的子序列一定是单调的。

算法的时间复杂度为 $O(n ^ 2)$，但由于其排序利用的性质，插入排序在大量递增的数据面前能有较好的表现。

1
2
3
4
5
6
7
8
9
10
void IS() {
    for (int i = 1; i < n; i++) {
        int x = a[i], j = i - 1;
        while (j >= 0 && a[j] > x) {
            a[j + 1] = a[j];
            j--;
        }
        a[j + 1] = x;
    }
}
2. 自顶向下归并排序（Top-down Mergesort，TDM）

由于大的序列排序问题可以分解为其子序列的排序子问题（分治法），故可以将目前的 $[l, r]$ 区间划分为 $[l, mid]$ 和 $[mid + 1, r]$，递归处理。递归回溯过后的这两段区间一定是有序的，进而可以合并这两个子区间，来得到排序过后的 $[l, r]$。

合并的方法即每次取这两个子序列中较小的那个数字，依次放到新的序列里。最后还需要把未放完的子序列中的数字集体放入新序列中。这样得到的新序列一定是有序的。

算法的时间复杂度为 $O(n \log n)$，是一种比较稳定且优秀的排序方法，并且还有一些应用（e.g. 计算某个序列中的逆序对个数）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void TDM(int l, int r) {
	if (l == r) return ;
	int mid = (l + r) / 2;
	TDM(l, mid);
	TDM(mid + 1, r);
	int i = l, j = mid + 1, k = l;
	while (i <= mid && j <= r) {
		if(a[i] > a[j]) b[k++] = a[j++];
		else b[k++] = a[i++];
	}
	while (i <= mid) b[k++] = a[i++];
	while (j <= r) b[k++] = a[j++];
	for (int k = l; k <= r; k++) a[k] = b[k];
}
3. 自底向上归并排序（Bottom-up Mergesort，BUM）

与 TDM 不同，我们也可以把小的有序序列们依次合并成大的有序序列，这样也可以实现整体的排序。元素的个数可以采用 $2$ 的整数次幂，这样的子序列的长度也比较平均。

算法的时间复杂度为 $O(n \log n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void merge(int l, int mid, int r) {
    int n1 = mid - l + 1, n2 = r - mid;
    vector<int> b(n1 + 5), c(n2 + 5);
    for (int i = 1; i <= n1; i++) b[i] = a[l + i - 1];
    for (int i = 1; i <= n2; i++) c[i] = a[mid + i];
    int i = 1, j = 1, k = l;
    while (i <= n1 && j <= n2) {
        if (b[i] <= c[j]) a[k++] = b[i++];
        else a[k++] = c[j++];
    }
    while (i <= n1) a[k++] = b[i++];
    while (j <= n2) a[k++] = c[j++];
}

void BUM() {
    for (int now = 1; now <= n; now <<= 1) {
        for (int l = 1; l <= n; l += 2 * now) {
            int mid = min(l + now - 1, n), r = min(l + 2 * now - 1, n);
            merge(l, mid, r);
        }
    }
}
4. 随机快速排序（Random Quicksort，RQ）

快速排序与归并排序（Merge Sort）一样，采用了分治的思想，在每次处理区间的时候，选取一个基准值 $pivot = a[x]$，让 $pivot$ 左边所有数字都小于它本身，让 $pivot$ 右边所有数字都大于它本身。然后再去递归基准值左右两边的区间。

不难发现排序的快慢会受到 $pivot$ 选取策略的影响。随机的去选择 $pivot$ 可以让排序的效率不被输入数据的顺序、大小的特点而明显影响到。

算法的时间复杂度为 $O(n \log n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void RQ(int l, int r) {
	if(l >= r) return ;
	int i = l, j = r, pivot = a[l + rand() % (r - l + 1)];
	while(i <= j) {
		while(a[i] < pivot) i++;
		while(a[j] > pivot) j--;
		if(i <= j) {
			swap(a[i], a[j]);
			i++;
			j--;
		}
	}
	RQ(l, j);
	RQ(i, r);
}
5. Dijkstra 3-路划分快速排序（Quicksort with Dijkstra 3-way Partition，QD3P）

QD3P 也使用了基准数 $pivot$ 的概念，将数组分成三个部分：小于 $pivot$ 的部分、等于 $pivot$ 的部分和大于 $pivot$ 的部分。然后递归地对这三个部分分别进行排序，以完成整个排序过程。在处理包含大量重复元素的数据时会展现出优秀的性能。

算法的时间复杂度为 $O(n \log n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void QD3P(int l, int r) {
    if (l >= r) return ;
    int lt = l, gt = r, i = l + 1, pivot = a[l];
    while (i <= gt) {
        if (a[i] < pivot) {
            swap(a[lt], a[i]);
            lt++;
            i++;
        }
        else if (a[i] > pivot) {
            swap(a[i], a[gt]);
            gt--;
        }
        else i++;
    }
    QD3P(l, lt - 1);
    QD3P(gt + 1, r);
}
测量时间与空间占用量

笔者在此次实验中采用了线上评测系统来更方便的去测试不同排序程序在不同规模数据下的性能表现。即先在本地通过数据生成器，将不同规模、不同特点的数据打包上传至评测系统的服务器，再将各个排序的程序分别提交，查看运行时候的时间、空间占用量。

本次线上评测系统选择的是洛谷平台，洛谷平台为用户提供了「创建题目」以及「提交测评」的功能。

评测结果界面：

20db3d30be58146658c09c1962380cf9.png

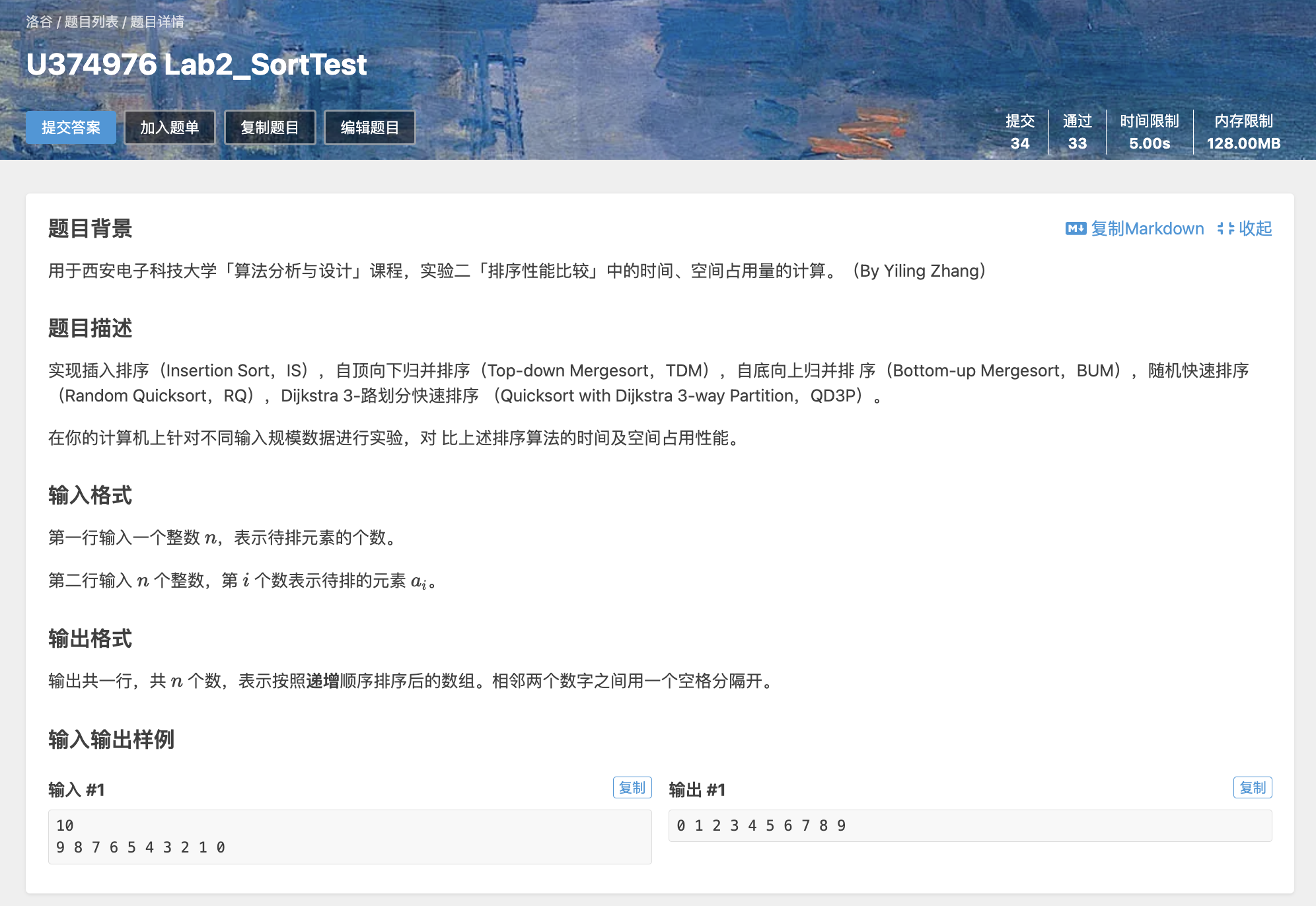
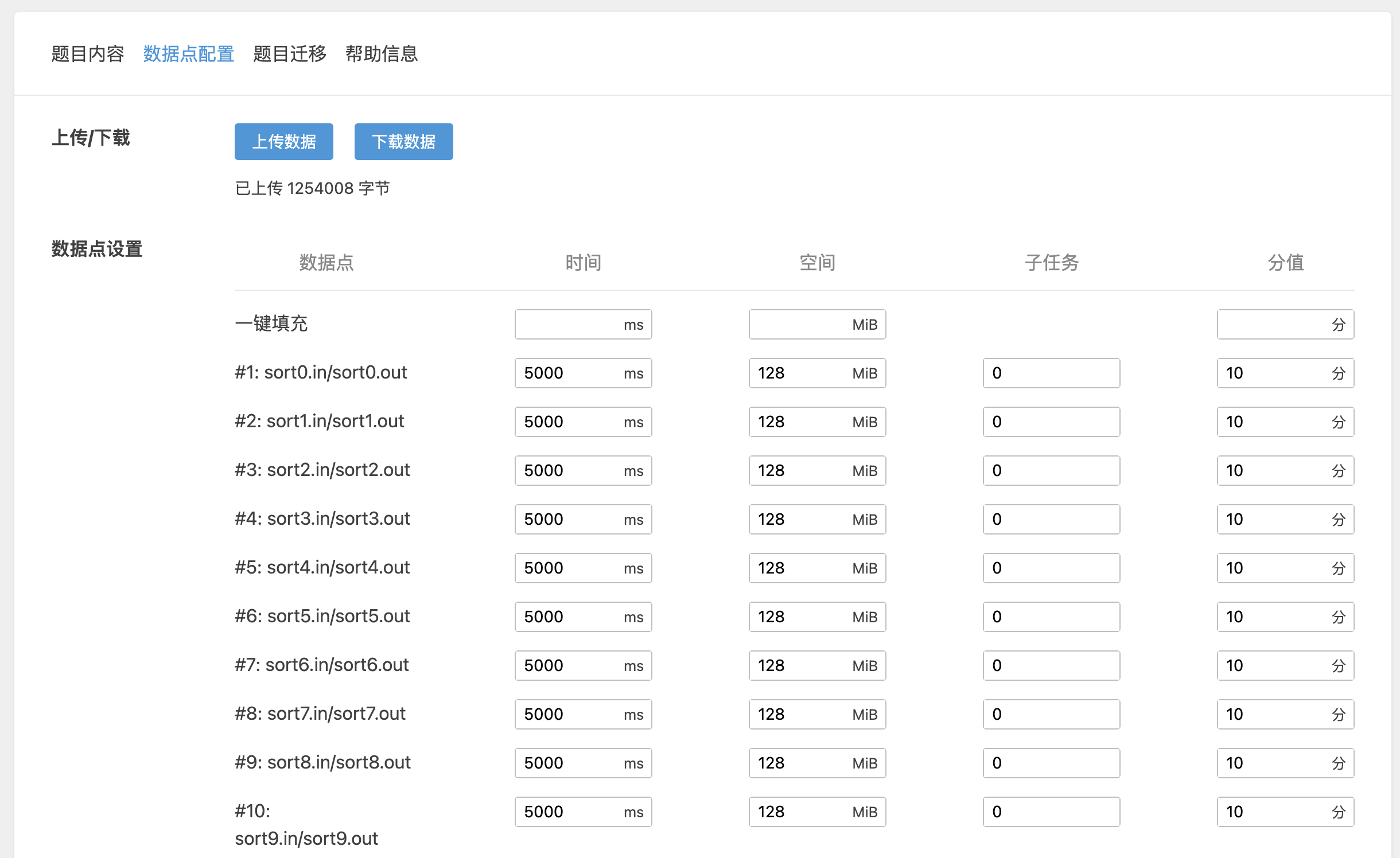
以下是用于此次评测的题目的相关信息：

3c831a00b72ff229fa2cecc9859cfa0f.png

a48afde36ec35ac5574632181f273368.png

本地的数据生成器（generator.cpp）代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;

int a[20050];

void solve1() {
    for (int i = 1; i <= n; i++) cout << rand() % 50 << (i == n ? "\n" : " ");
}
// generate random data

void solve2() {
    int m = 0;
    for (int i = 1; i <= n; i++) {
        int x = rand() % 100;
        a[++m] = x;
    }
    sort(a + 1, a + m + 1);
    for (int i = 1; i <= m; i++) cout << a[i] << (i == m ? "\n" : " ");
} 
//generate data which has been sorted

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
	srand(time(0)); // for random data
    freopen("sort.in", "w", stdout); // write the generated data in the file
    int n = 20000, type; // set the number of data
    cout << n << endl;
    cin >> type;
    type ? solve1() : solve2(); // choose different kinds of data
    return 0;
}

本地的排序过后（sort.cpp）的数据生成器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <bits/stdc++.h>
using namespace std;
int n, a[20050];
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    freopen("sort0.in", "r", stdin);
    freopen("sort0.out", "w", stdout); // generate the right answer after sorting
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort (a + 1, a + n + 1);
    for (int i = 1; i <= n; i++) cout << a[i] << (i == n ? "\n" : " ");
    return 0;
}

运用线上评测的优势是方便查看时间、空间的占用量，并且能够检测程序的正确性。缺点是显示精度取决于评测提供方，结果可能不够精确。

四. 结果分析

1. 大量有序数据（N = 20000）

时间占用（单位：$\mu s$）：

6b5f8064b9c857dca7a5523feb426771.png

空间占用（单位：$kb$）：

da536b2e2cbd1e80dcb0a0644b42312a.png

2. 大量重复数据（N = 20000）

时间占用（单位：$\mu s$）：

297749772dce5a9d48d6db88c1c2551b.png

空间占用（单位：$kb$）：

ea73251725d77acadd2192351896ce25.png

3. 大量随机数据（N = 20000）

时间占用（单位：$\mu s$）：

3b05d1b1fd43dba843d7bc7957d2f3ec.png

空间占用（单位：$kb$）：

04e3d4449a303fd3e9230bc9ab38e334.png

4. 少量随机数据（N = 1000）

时间占用（单位：$\mu s$）：

b6cd7c15857a275c28a789968e887a88.png

空间占用（单位：$kb$）：

390a7c71375997f3673f1d7496dcb2fd.png

五. 问题回答

  1. Which sort worked best on data in constant or increasing order (i.e., already sorted data)? Why do you think this sort worked best?
    (1). Insertion Sort. In the first test, Insertion Sort solves the problem the fastest.
    6b5f8064b9c857dca7a5523feb426771.png
    (2). This is because when the sequence is already sorted, everytime we want to arrange this element to its right position, we can add it to the final sequence directly. Its time complexity turns to $O(n)$.

  2. Did the same sort do well on the case of mostly sorted data? Why or why not?
    (1). For Insertion Sort, it runs much more faster than it runs on the random situation. The reason why has been explained in last question.
    3451d992cd1caa0f24e64ae6ac727bea.png
    (2). For QD3P, it runs much more slower than it runs on the mostly repeated situation.
    a9d05c65db3968027f730cf3df26a5ce.png

  3. In general, did the ordering of the incoming data affect the performance of the sorting algorithms? Please answer this question by referencing specific data from your table to support your answer.
    (1). Yes.
    (2). For QD3P, when the data is generated randomly, the cost of time is much more shorter than it runs on sorted data.
    95b498a0cfc7a5682d9d3fb4b70335cf.png

  4. Which sort did best on the shorter (i.e., n = 1,000) data sets? Did the same one do better on the longer (i.e., n = 100,000) data sets? Why or why not? Please use specific data from your table to support your answer.
    (1). When $n$ is not very large (e.g. n = 1000), different algorithms takes almost same time to sort.
    b6cd7c15857a275c28a789968e887a88.png
    (2). When $n$ is very large, which algorithm works best depends on whether the data is already sorted and the number of repeated number in the data set. Theoretically speaking, QD3P works best in most condition, especially when there are many repeated elements in the data set. But there are also some speical cases.

  5. In general, which sort did better? Give a hypothesis as to why the difference in performance exists.
    (1). QD3P works best in most condition.
    (2). The performance depends on many aspects, including the size of data, whether the sequence is already sorted, and whether it will use the space of system stack and so on.

  6. Are there results in your table that seem to be inconsistent? (e.g., If I get run times for a sort that look like this {1.3, 1.5, 1.6, 7.0, 1.2, 1.6, 1.4, 1.8, 2.0, 1.5} the 7.0 entry is not consistent with the rest). Why do you think this happened?
    (1). I think it is related to the data and system environment.

算法分析与设计 - Lab2 - 排序算法的性能比较

http://example.com/2023/10/27/算法分析与设计-Lab2-排序算法的实验性能比较/

作者

Zylll

发布于

2023-10-27

更新于

2023-10-27

许可协议

#
×