发表更新专业知识13 分钟读完 (大约1969个字)

算法分析与设计 - Lab1 - 渗透问题

一．实验目的

使用并查集(union-find)数据结构，编写程序通过蒙特卡罗模拟(Monte Carlo simulation)来估计渗透阈值。

二．实验内容

给定由随机分布的绝缘材料和金属材料构成的组合系统:金属材料占多大比例才能使组合系统成为电导体? 给定一个表面有水的多孔景观(或下面有油)，水将在什么条件下能够通过底部排出(或油渗透到表面)? 科学家已经定义了一个称为渗透(percolation)的抽象过程来模拟这种现象。

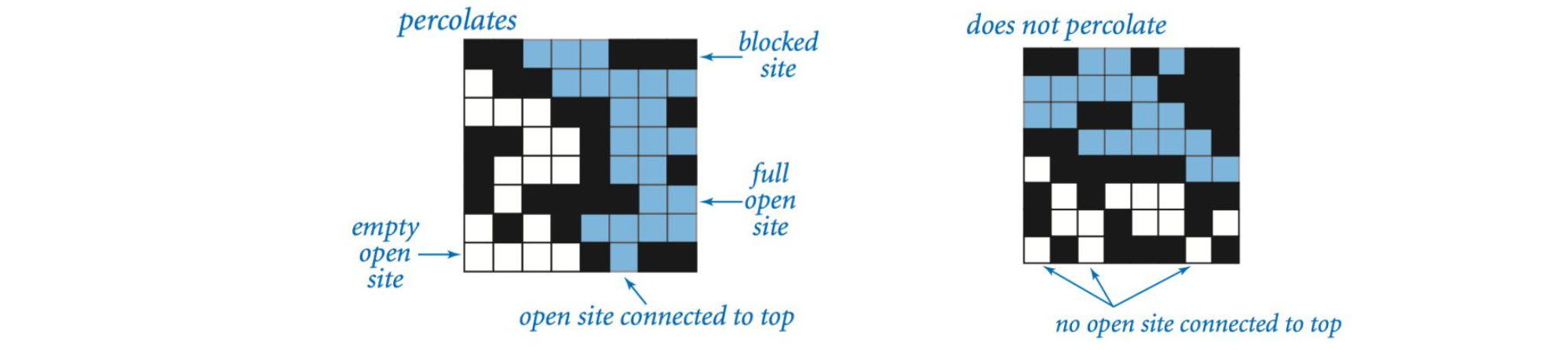
我们使用 $N \times N$ 网格点来模型化一个渗透系统。 每个格点或是 open 格点或是 blocked 格点。 一个 full site 是一个 open 格点，它可以通过一系列的邻近(左、右、上、下) open 格点连通到顶行的一个 open 格点。如果在底行中有一个 full site 格点，则称系统是渗透的。(对于绝缘/金属材料的例子，open 格点对应于金属材料，渗透系统有一条从顶行到底行的金属材料路径，且 full sites 格点导电。对于多孔物质示例，open 格点对应于空格，水可能流过，从而渗透系统使水充满 open 格点，自顶向下流动。)

pPOeKaD.png

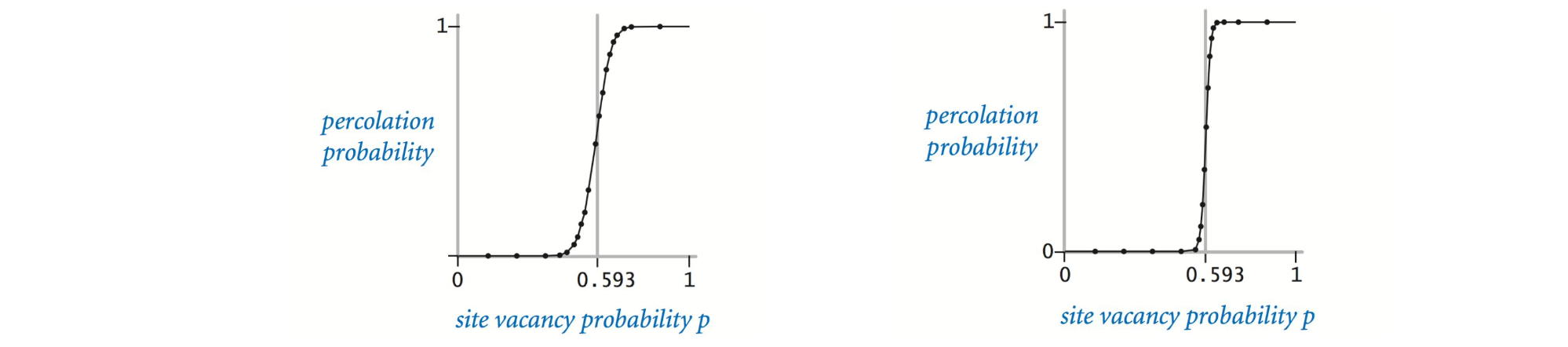
在一个著名的科学问题中，研究人员对以下问题感兴趣:如果将格点以概率 $p$ 独立地设置为 open 格点(因此以概率 $1-p$ 被设置为 blocked 格点)，系统渗透的概率是多少? 当 $p = 0$ 时，系统不会渗出; 当 $p = 1$ 时，系统渗透。下图显示了 $20 \times 20$ 随机网格（左）和 $100 \times 100$ 随机网格（右）的格点空置概率 $p$ 与渗滤概率。

pPOeuVO.png

当 $N$ 足够大时，存在阈值 $p*$，使得当 $p < p \ast$ ，随机 $N \times N$ 网格几乎不会渗透，并且当 $p > p \ast$ 时，随机 $N \times N$ 网格几乎总是渗透。尚未得出用于确定渗滤阈值 $p \ast$ 的数学解。你的任务是编写一个计算机程序来估计 $p \ast$。

蒙特卡洛模拟(Monte Carlo simulation). 要估计渗透阈值，考虑以下计算实验:

  1. 初始化所有格点为 blocked。
  2. 重复以下操作直到系统渗出:
    2.1. 在所有 blocked 的格点之间随机均匀选择一个格点 $(i, j)$。
    2.2. 设置这个格点 $(i, j)$ 为 open 格点。

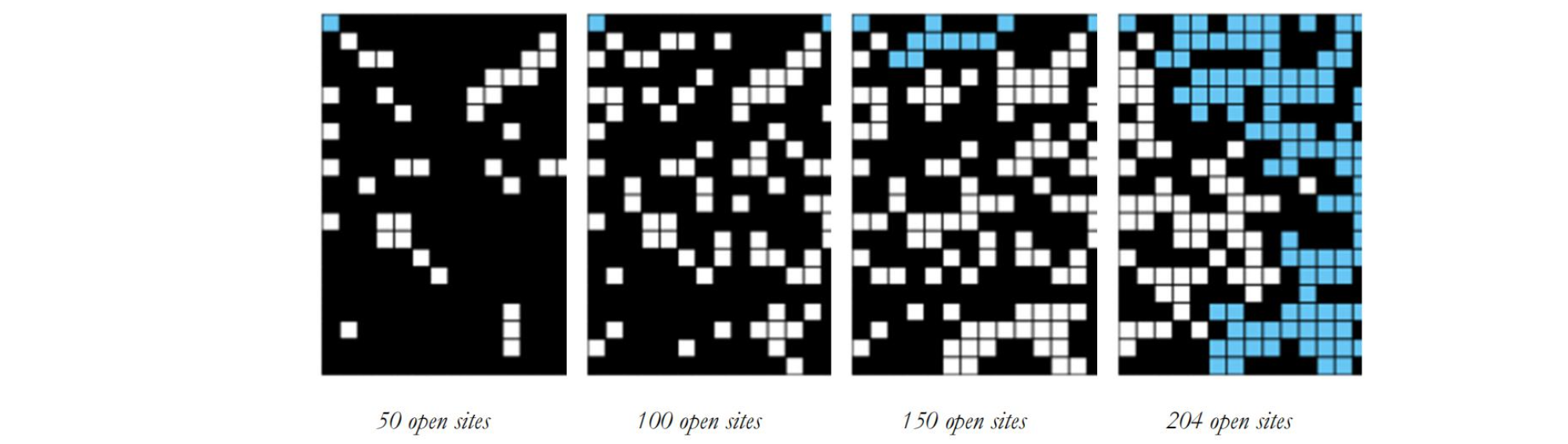
open 格点的比例提供了系统渗透时渗透阈值的一个估计。例如，如果在 $20 \times 20$ 的网格中，根据以下快照的 open 格点数，那么对渗滤阈值的估计是 $\frac{204}{400} = 0.51$， 因为当第 $204$ 个格点被 open 时系统渗透。

pPOeMIe.png

通过重复该计算实验 $T$ 次并对结果求平均值，我们获得了更准确的渗滤阈值估计。 令是第 $x_t$ 次计算实验中 open 格点所占比例。样本均值提供渗滤阈值的一个估计值; 样本标准差测量阈值的灵敏性。

$$
\mu = \frac{\sum_{i = 1}^{T}x_i}{T}, \quad \sigma^2 = \frac{\sum_{i = 1}^{T}(x_i - \mu) ^ 2}{T - 1}
$$

假设 $T$ 足够大，以下为渗滤阈值提供 $95%$ 置信区间:

$$
[\mu - \frac{1.96 \sigma}{\sqrt{T}}, \mu + \frac{1.96 \sigma}{\sqrt{T}}]
$$

三．实验过程

并查集

根据题意，在实验中，可以把首行中的 $n$ 个点由一个特殊点（编号为 $0$）来代替。即在并查集的初始化过程中，把第一行的 $n$ 个点都指向 $0$ 号点。最后一行也同理。

如何给 $N \times N$ 个点编号？可以采用“先行后列，同时新的一行的第一个点保留”的方法来排号。“保留”的目的是我们需要把第一行、最后一行（第 $N$ 行）的所有点都分别指向对应的特殊点。采用这种方法，可以很方便的通过某个点的行号 $i$ 和列号 $j$ ，推导出其在这种方式下的真正编号。不难得出，$(i, j)$ 的真正编号为 $(i - 1) \cdot (N + 1) + j$。第一行的点全被指向 $0$ 号点，第 $N$ 行的所有点全被指向 $N ^ 2 - 1$ 号点，其余所有点最开始都指向自己。

同时本人在并查集中采用了路径压缩、按秩合并的技巧，减少了算法的时间复杂度。

该部分的源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int get_id(int i, int j) { return 1 + (i - 1) * (N + 1) + (j - 1); }

struct union_find_set {

    int fa[MAXN * MAXN], rk[MAXN * MAXN];

    int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); }
    // path compression

    bool connected(int x, int y) { return find(x) == find(y); }

    void initial() {
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                int id = get_id(i, j);
                fa[id] = id;
                rk[id] = 1;
                if (i == 1 || i == N) fa[id] -= j;
            }
        }
        fa[top_id] = top_id;
        fa[bottom_id] = bottom_id;
        rk[top_id] = rk[bottom_id] = 2;
    }

    void unite(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy) return ;
        if (rk[fx] < rk[fy]) fa[fx] = fy;
        else {
            fa[fy] = fx;
            if (rk[fx] == rk[fy]) rk[fx]++;
        }
    }
    // weighted quick-union

}s1;

注意到实验中还需要分析不带按秩合并的并查集在运行相同规模数据时候的表现，只需要在上述代码中的 initial 和 unite 部分中去除与 rk 有关的代码即可（ unite 中直接合并）。在这里不再赘述。

Percolations 与 PercolationStats 类

结合题意，本人用 struct 创建了对应的数据类型及接口。

Percolations 部分的源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Percolations {

    struct node {
        int id, sta;
    }a[MAXN][MAXN];

    bool isOpen(int i, int j) { return a[i][j].sta; }
    // is site (row i, column j) open?
    
    void open(int i, int j) { a[i][j].sta = 1; }
    // open site (row i, column j) if it is not already

    bool percolates() { return s1.connected(top_id, bottom_id); }
    // does the system percolate?

    void Percolation(int N) {
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                a[i][j].sta = 0;
                a[i][j].id = get_id(i, j);
            }
        }
    }
    // create N-by-N grid, with all sites blocked

}now;

PercolationStats 部分的源代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
struct PercolationStats {
    
    const int dirx[5] = {0, 0, 0, 1, -1};
    const int diry[5] = {0, 1, -1, 0, 0};

    double res, ave, sigma, sigma_squ;
    std::vector<double> esti_p;

    bool check_out(int i, int j) { return i < 1 || j < 1 || i > N || j > N; }
    // check whether (i, j) is out of the grid

    double mean() { return res / T; }
    // sample mean of percolation threshold
    
    double variance() {
        double val = 0;
        for (auto x : esti_p) val += pow((x - ave), 2);
        return val / (T - 1);
    }
    // sample variance of percolation threshold

    double stddev() { return sqrt(sigma_squ); }
    // sample standard deviation of percolation threshold

    double confidenceLo() { return ave - (1.96 * sigma) / sqrt(T); } 
    // returns lower bound of the 95% confidence interval

    double confidenceHi() { return ave + (1.96 * sigma) / sqrt(T); }
    // returns upper bound of the 95% confidence interval 

    void PercolationStat(int N, int T) {
        for (int k = 1; k <= T; k++) {
            now.Percolation(N);
            s1.initial();
            int cnt = 0;
            while (!now.percolates()) {
                int nx = rand() % N + 1, ny = rand() % N + 1;
                if (!now.isOpen(nx, ny)) {
                    cnt++;
                    now.open(nx, ny);
                }
                for (int i = 1; i <= 4; i++) {
                    int dx = nx + dirx[i], dy = ny + diry[i];
                    if (check_out(dx, dy)) continue;
                    if (now.isOpen(dx, dy)) {
                        int idu = get_id(dx, dy), idv = get_id(nx, ny);
                        s1.unite(idu, idv);
                    }
                }
            }
            double nowp = 1.0 * cnt / (N * N);
            esti_p.push_back(nowp);
            res += nowp;
        }
    }
    // perform T independent computational experiments on an N-by-N
    
    void Calculation() {
        ave = mean();
        sigma_squ = variance();
        sigma = stddev();
        std::cout << "mean = " << ave << "\n";
        std::cout << "stddev = " << sigma << "\n";
        std::cout << "95% confidence interval is [" << confidenceLo() << ", " << confi
        denceHi() << "]" << "\n";
    }
    // calculate the mean, stddev, and the confidence interval of this experiment

}lab;

四. 结果分析

quick-find 运行表现

N = 200, T = 100:

2023-10-09-11.09.54.png
2023-10-09-11.09.59.png

N = 2, T = 100000:

2023-10-09-11.10.03.png

N = 300, T = 500:

2023-10-09-11.10.19.png

weighted quick-find 运行表现

N = 200, T = 100:

pPOmkTS.png
pPOmEFg.png

N = 2, T = 100000:

pPOmVYQ.png

N = 300, T = 500:

pPOmFw8.png

不难发现在较大规模数据的时候，按秩合并优化对程序时间的减少效果是明显的。

算法分析与设计 - Lab1 - 渗透问题

http://example.com/2023/10/26/算法分析与设计-Lab1-渗透问题/

作者

Zylll

发布于

2023-10-26

更新于

2023-10-26

许可协议

#

目录

×