抽象代数笔记

6.1 代数结构

代数系统（代数）：非空集合 $S$ 和 $S$ 上的 $k$ 个一元或二元运算 $f_1, f_2, \cdots f_k$ 组成的系统。记作 $ \langle S, f_1, f_2, \cdots, f_k \rangle$ 。

6.1.1 代数运算

设 $A, B$ 是非空集合， $f$ 是从 $A ^ n$ 到 $B$ 的一个映射，则称 $f$ 为集合 $A ^ n$ 到 $B$ 的一个 $n$ 元代数运算。（其中 $n$ 称作该运算的阶）。
$+, -, \ast, \circ$ 等这些符号加上 普通 的前缀，才代表的是其原来的运算。

运算的封闭性

设 $f$ 为集合 $A ^ n$ 到 $B$ 的一个 $n$ 元运算。若 $B \subseteq A $ ,则称 $f$ 在集合 $A$ 上是封闭的。
e.g. 普通减运算在 $\mathbb N$ 上不封闭。

若称一个运算是某个集合上的运算，则该运算必须满足在这个集合上具有封闭性。

1. 运算性质 - 交换律

设 $\ast$ 为 $S$ 上的二元运算，若 $ \forall x, y \in S$ 都有：

$$
x \ast y = y \ast x
$$

则称运算 $ \ast $ 在 $S$ 上可交换。
若已知该运算的运算表，则可通过判断该表是否满足沿主对角线对称，来判断是否满足交换律。

2. 运算性质 - 结合律

设 $\ast$ 为 $S$ 上的二元运算，若 $ \forall x, y, z \in S$ 都有:

$$
(x \ast y) \ast z = x \ast (y \ast z)
$$

则称运算 $\ast$ 在 $S$ 上可结合。
判断该运算是否满足结合律，不能通过运算表直观的看出来。

3. 运算性质 - 分配律

设 $\ast, \circ$ 为 $S$ 上的二元运算，若 $ \forall x, y, z \in S$ 都有：

$$
x \ast (y \circ z) = (x \ast y) \circ (x \ast z), \quad 称 \ast 对 \circ 左可分配 \
(y \circ z) \ast x = (y \ast x) \circ (z \ast x), \quad 称 \circ 对 \ast 右可分配
$$

则称 $\ast$ 对 $\circ$ 可分配。

4. 运算性质 - 吸收律

设 $\ast, \circ$ 为 $S$ 上的二元运算，若 $ \forall x, y \in S$ 都有：

$$
x \ast (x \circ y) = x, \quad 称 \ast 对 \circ 左可吸收 \
(x \circ y) \ast x = x, \quad 称 \circ 对 \ast 右可吸收
$$

则称 $\ast$ 对 $\circ$ 可吸收。
若 $\ast$ 满足交换律，则只需证明一边满足吸收律即可。
e.g. 集合中的 $\bigcup$ 运算对 $\bigcap$ 运算可吸收。因为 $A \bigcup (A \bigcap B) = A$（右可吸收同理）。

5. 运算性质 - 等幂律

设 $\ast$ 为 $S$ 上的二元运算，若 $ \forall x \in S$ 都有:

$$
x \ast x = x
$$

则称运算 $\ast$ 在 $S$ 上满足等幂律。

6. 运算性质 - 消去律

设 $\ast$ 为 $S$ 上的二元运算，某个元素 $a \in S$，若 $ \forall x, y \in S$ 都有：

$$
a \ast x = a \ast y \ \Rightarrow x = y, \quad 称a是左可消去的 \
x \ast a = y \ast a \ \Rightarrow x = y, \quad 称a是右可消去的
$$

则称 $a$ 关于 运算 $\ast$ 是可消去的。
若 $S$ 中所有的元素都满足消去律，则可说明 $\ast$ 满足消去律。

$a \ast x = a \ast y \ \Rightarrow x = y$ 叫做永真蕴含式。箭头左边的式子叫做前件，右边的叫做后件。永真蕴含式表明，若前件成立，则后件一定成立。永真蕴含式的逆否形式也成立。

可消去性可以从运算表中观察到。若 $\ast$ 满足消去律，则运算表中每一行每一列中都没有相同的元素。

6.1.2 代数常元

该代数系统中与运算相关的特殊元素称作代数常元。

1. 幺元

设 $\ast$ 是定义在 $S$ 上的二元运算，若存在元素 $e_l$ (或 $e_r$) 使得 $\forall x \in A$ 都有：

$$
e_l \ast x = x \quad （或 \ x \ast e_r = x）
$$

则称 $e_l$ (或 $e_r$) 是 $S$ 中关于 $\ast$ 运算的左（右）幺元。
若 $e$ 既是左幺元又是右幺元，则称 $e$ 是 $S$ 中关于 $\ast$ 运算的幺元。且 $e$ 是 $S$ 上关于 $\ast$ 的唯一的幺元。

2. 零元

设 $\ast$ 是定义在 $S$ 上的二元运算，若存在元素 $\theta_l$ (或 $\theta_r$) 使得 $\forall x \in A$ 都有：

$$
\theta_l \ast x = \theta_l \quad （或 \ x \ast \theta_r = \theta_r）
$$

则称 $\theta_l$ (或 $\theta_r$) 是 $S$ 中关于 $\ast$ 运算的左（右）零元。
若 $\theta$ 既是左零元又是右零元，则称 $\theta$ 是 $S$ 中关于 $\ast$ 运算的零元。且 $\theta$ 是 $S$ 上关于 $\ast$ 的唯一的零元。

3. 逆元

设 $\ast$ 是定义在 $S$ 上的二元运算，$e$ 是 $S$ 中关于 $\ast$ 运算的幺元。对于 $x \in S$, 如果存在 $y_l \in S$ （或 $y_r \in S$）使得：

$$
y_l \ast x = e \quad （或 \ x \ast y_r = e）
$$

则称 $y_l$ (或 $y_r$) 是 $x$ 的左（右）逆元。
若 $y \in S$ 既是左逆元又是右逆元，则称 $y$ 是 $x$ 的逆元。

若 $\ast$ 运算是可结合的，且对于 $x \in S$ 存在 $y_l, y_r$ ，则 $y$ 是 $x$ 的唯一的逆元, $y = y_l = y_r$。

6.2 子代数

6.2.1 子代数的定义

设 $\langle A, \ast, \varDelta, k \rangle$ 是一个代数系统， $\ast, \varDelta$ 分别是载体 $A$ 上的二元运算和一元运算， $k$ 是代数常元。若：

$$
A’ \subseteq A \ A’ 对 \ast 和 \varDelta 均封闭 \ k \subseteq A’
$$

则称 $\langle A, \ast, \varDelta, k \rangle$ 是 $A$ 的子代数系统。
若 $A’ = A$， $\langle A’, \ast, \varDelta, k \rangle$ 被称为 $A$ 的最大的子代数。
若 $A’ = k$， $\langle A’, \ast, \varDelta, k \rangle$ 被称为 $A$ 的最小的子代数。
最大和最小子代数被称为 $A$ 的平凡子代数。其余的子代数（$A’ \subseteq A$）被称为 $A$ 的真子代数。

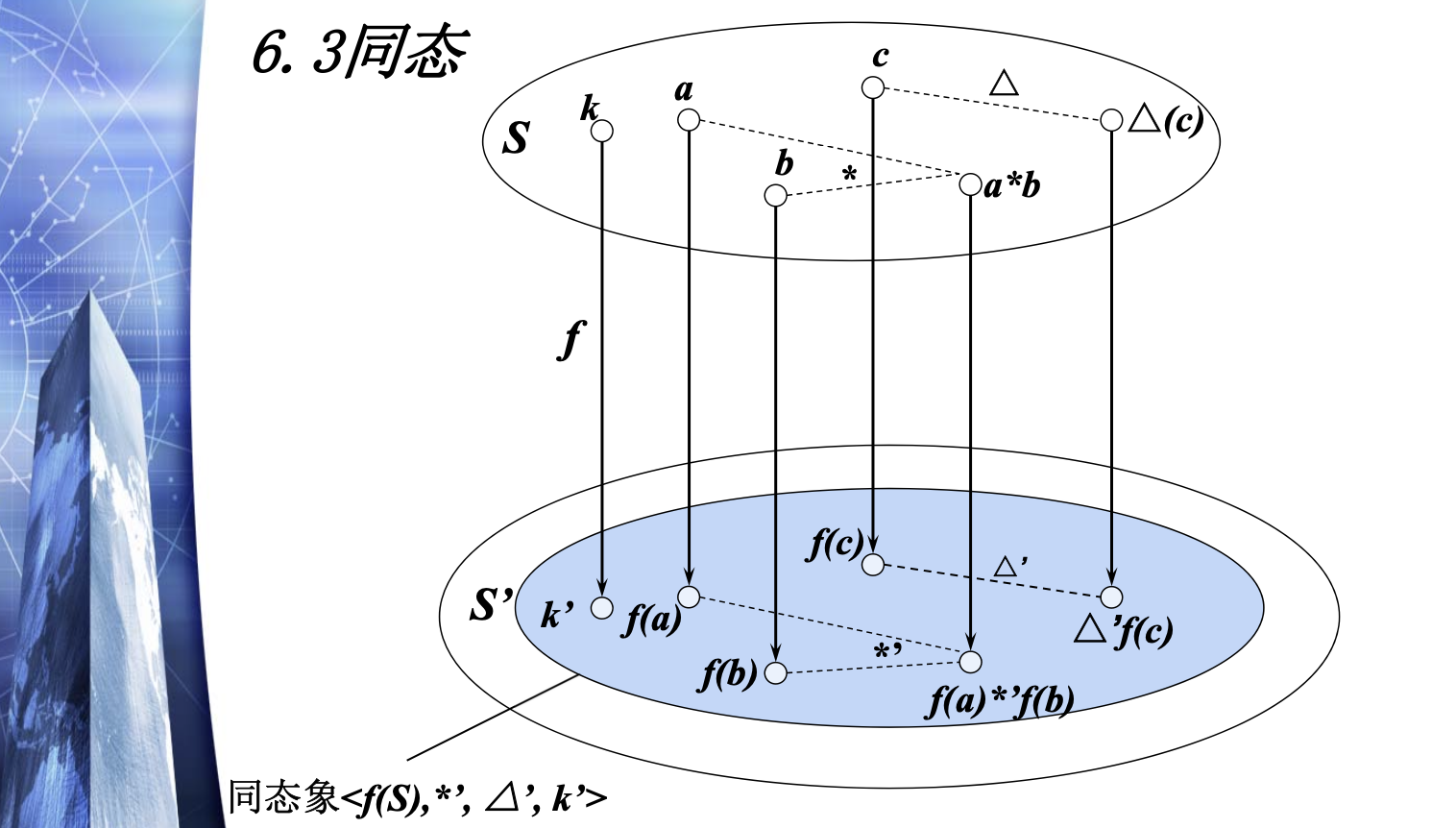
6.3 同态

6.3.1 同态的定义

设 $A = \langle S, \ast, \varDelta, k \rangle, A’ = \langle S’, \ast’, \varDelta’, k’ \rangle$ 两个具有相同构成的代数系统， $f$ 是从 $S$ 到 $S’$ 的一个映射， 且对 $\forall a, b \in S$ 满足（先运算再映射 = 先映射再运算）：

$$
f(a\ast b) = f(a) \ast’f(b) \ f(\varDelta a) = \varDelta’f(a) \ f(k) = k’
$$

则称 $f$ 为由 $A$ 到 $A’$ 的一个同态映射， 简称同态， 记作 $A \sim A’$。

6.3.2 同态象

设 $f$ 是从 $A$ 到 $A’$ 的同态映射，称 $\langle f(S), \ast’, \varDelta’, k’ \rangle$ 为 $A$ 在映射 $f$ 下的同态象。

6.3.3 同态的分类

设 $f$ 是从 $A$ 到 $B$ 的一个映射。

1. 满射：若 $B$ 中每个值都能在 $A$ 中找到其原象，则称 $f$ 是一个满射。
2. 单射：若 $\forall x, y \in A, x \neq y$，都有 $f(x) \neq f(y)$。则称 $f$ 是一个单射。
3. 双射：既是满射又是双射的映射。

设 $f$ 是从 $A = \langle S, \ast, \varDelta, k \rangle$ 到 $A’ = \langle S’, \ast’, \varDelta’, k’ \rangle$ 的一个同态映射。

1. 若 $f$ 是满射的，则称 $f$ 是一个满同态。
2. 若 $f$ 是单射的，则称 $f$ 是一个单一同态。
3. 若 $f$ 是双射的，则称 $f$ 是一个同构映射，简称同构，记作 $A \cong A’$。
4. 若 $A = A’$，则称 $f$ 为 $A$ 上的自同态。
5. 若 $A = A’$ 且 $f$ 是双射的，则称 $f$ 为 $A$ 上的自同构。

6.3.4 同态的性质

设 $f$ 是从 $A = \langle S, \ast, \varDelta, k \rangle$ 到 $A’ = \langle S’, \ast’, \varDelta’, k’ \rangle$ 的一个同态映射。那么 $A$ 的同态象 $A’’ = \langle f(S), \ast’, \varDelta’, k‘ \rangle$。

1. $A’’$ 是 $A’$ 的子代数。
2. 若 $\ast$ 在 $A$ 中可交换（可结合），则 $\ast’$ 在 $A’’$ 中也可交换（可结合）。
3. 若在 $A$ 中 $\ast$ 对 $\varDelta$ 可分配，则在 $A’’$ 中 $\ast’$ 对 $\varDelta’$ 也可分配。
4. 若 $e$ 是 $A$ 中关于运算 $\ast$ 的幺元，则 $f(e)$ 也是 $A’’$ 中关于运算 $\ast’$ 的幺元。
5. 若 $\theta$ 是 $A$ 中关于运算 $\ast$ 的零元，则 $f(\theta)$ 也是 $A’’$ 中关于运算 $\ast’$ 的零元。
6. $\forall x \in S$, $x$ 对运算 $\ast$ 存在逆元 $x^{-1}$；则在 $f(S)$ 中，$f(x)$ 也有关于运算 $\ast’$ 的逆元 $f(x^{-1})$。

6.4 同余

6.4.1 同余的定义

设代数系统 $A = \langle S, \ast, \varDelta \rangle$ ， $ \sim $ 是载体 $S$ 上的等价关系。 $\forall a, b, c, d \in S：$

1. 当 $a \sim b$ 时，若 $\varDelta a \sim \varDelta b$，则说明等价关系在一元运算 $\varDelta$ 下是可保持的，称 $\sim$ 是关于运算 $\varDelta$ 的同余关系。

2. 当 $a \sim b, c \sim d$ 时，若 $a \ast c \sim b \ast d$，则说明等价关系在二元运算 $\ast$ 下是可保持的，称 $\sim$ 是关于运算 $\ast$ 的同余关系。

若 $\sim$ 在 $A$ 上的所有运算下都是可保持的，则称 $\sim$ 是代数系统 $A$ 上的同余关系。

等价关系具有对称性、自反性、传递性。

6.4.2 与同态有关的定理

设 $g$ 是从 $A = \langle S, \ast, \varDelta, k \rangle$ 到 $A’ = \langle S’, \ast’, \varDelta’, k’ \rangle$ 的一个同态映射。若在 $A$ 上定义等价关系 $R$ ：

$$
\langle a, b \rangle \in R, \quad iff: g(a) = g(b)
$$

则 $R$ 是 $A$ 上的一个同余关系。

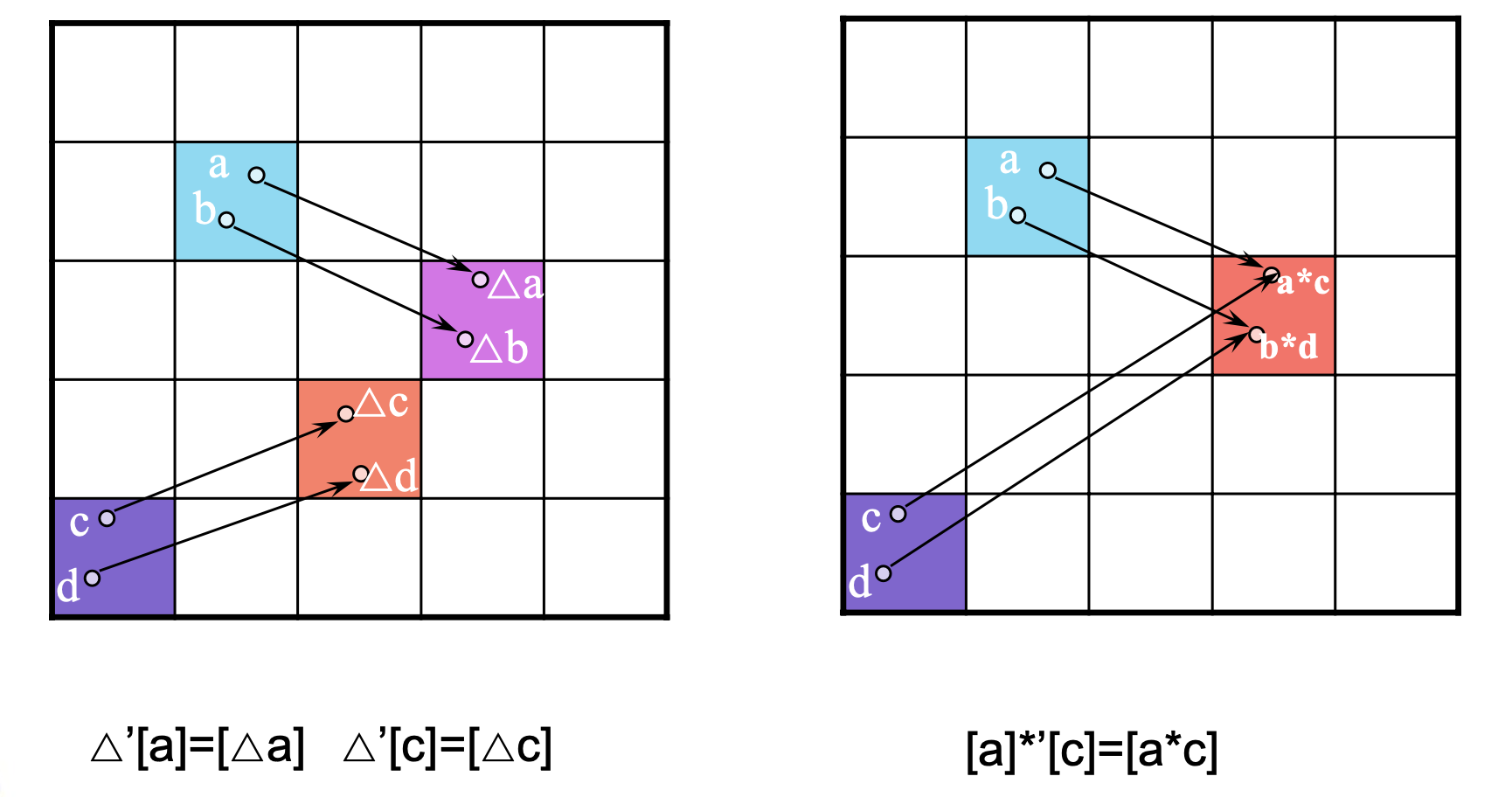
6.5 商代数

6.5.1 商代数的定义与性质

设代数系统 $A = \langle S, \ast, \varDelta, k \rangle$，$\sim$ 是 $A$ 上的同余关系。
则称 $A$ 关于 $\sim$ 的商代数 $A/ ! \sim \ = \langle S/ ! \sim, \ast’, \varDelta’, [k] \rangle$。其中 $ \varDelta’[a] = [\varDelta a], \ [a] \ast’ [b] = [a \ast b]$。

$S/ ! \sim$ 是集合的集合，即等价类的集合。该集合是 $S$ 的一个划分，即该集合中任意两元素（集合）的交集是空集（因为等价具有传递性）。$\ast’, \varDelta’$ 是集合间的运算，$[k]$ 是代数常元的集合。

小结：由等价关系 $R$ 可以得到代数系统 $A$ 的载体的一个划分，以这个划分为新的载体，按照原运算的规则建立等价类之间新的运算，这样得到的代数系统是原代数系统的商代数。

6.6 半群与独异点

6.6.1 半群与子半群

半群：对于一个代数系统 $\langle S, \ast \rangle$， $\ast$ 是 $S$ 上的二元运算，若运算 $\ast$ 是可结合的，则称 $\langle S, \ast \rangle$ 为半群。
子半群：设 $\langle S, \ast \rangle$ 是一个半群， $T \subseteq S$ 且 $\ast$ 在 $T$ 上是封闭的，那么 $\langle T, \ast \rangle$ 是 $\langle S, \ast \rangle$ 的子代数。$\langle T, \ast \rangle$ 也是一个半群，称为 $\langle S, \ast \rangle$ 的子半群（因为结合律在子代数上可继承）。

6.6.2 独异点与子独异点

独异点：含有幺元的半群（含幺半群）。
子独异点：满足是原代数系统的子代数，本身是独异点，且在相同运算下与原代数系统有相同幺元，那么称为是原独异点的子独异点。

6.6.3 半群与独异点的等幂元性质

设 $\langle S, \ast \rangle$ 是一个半群，若 $S$ 是一个有限集，则必存在 $a \in S$，使得 $a \ast a = a$。
证明：结合鸽巢原理。

6.6.4 交换半群与循环独异点

交换半群（独异点）：在半群（独异点）中，若运算是可交换的，则称此半群（独异点）为交换半群（独异点）。

循环独异点：设 $\langle S, \ast, e \rangle$ 是一个独异点，若 $\exists g \in S$ ，则 $ \forall a \in S , \exists k \in \mathbb N$ 使得 $a = g ^ k$ （$g ^ k$ 是 $k$ 个 $g$ 做运算的意思），则称此独异点为循环独异点。 （存在一个数能把其他所有数都表示出来）
$g$ 称为该循环独异点的生成元，一个循环独异点的生成元个数可以不唯一。

6.7 群

6.7.1 群的定义

群：设 $\langle G, \ast \rangle$ 是一个代数系统。若 $\ast$ 运算是可结合的（是半群），并且存在幺元（是独异点），并且 $\forall x \in G$，都存在其唯一的逆元 $x ^ {-1} \in G$，则称 $\langle G, \ast \rangle$ 是一个群。

群的阶数：群的元素个数，记作 $|G|$ 。
根据 $|G|$ 可以将群分为有限群和无限群。

6.7.2 群的性质

1. 群中无零元。
   （因为零元不可逆，故群中一定不含零元。）

2. 群中每个元素的逆元唯一。

3. 设 $\langle G, \ast \rangle$ 是一个群，对于 $a, b \in G$，必存在唯一的 $x \in G$，使得 $a \ast x = b$。
   （即群中任何两个元素都能通过运算相互表示。）

4. 设 $\langle G, \ast \rangle$ 是一个群， $\forall a, b, c \in G$，若有 $a \ast b = a \ast c$ 或者 $b \ast a = c \ast a$，则必有 $b = c$（消去律）。
   （因为没有零元，所以可以直接消去。）

5. 设 $\langle G, \ast \rangle$ 是一个群，除幺元 $e$ 外，不可能有任何别的等幂元。
   （幺元是唯一的等幂元。）

6. 群 $\langle G, \ast \rangle$ 的运算表的每一行/每一列都是 $G$ 中所有元素的一个置换。
   （$G$ 中每一个元素都会在运算表中的每一行/每一列出现，并且只出现一次。）

6.7.3 群中元素的阶

设 $\langle G, \ast \rangle$ 是一个群， $e$ 是幺元， $a \in G$。若存在唯一且最小的正整数 $n$ 使得 $a ^ n = e$，则称 $n$ 为元素 $a$ 的阶（或周期）；否则称元素 $a$ 的阶是无限的。

定理1

若群 $\langle G, \ast \rangle$ 的元素 $a$ 拥有一个有限阶 $n$ ，则 $a ^ k = e$ 当且仅当 $k$ 是 $n$ 的倍数。

定理2

群中任何一个元素 $a$ 与它的逆元 $a^{-1}$ 都具有相同的阶。

定理3

有限群 $\langle G, \ast \rangle$ 中任何一个元素的阶最多是 $|G|$。

6.7.4 阿贝尔群与循环群

阿贝尔群：若群 $\langle G, \ast \rangle$ 中 $\ast$ 运算是可交换的，则称该群为阿贝尔群（Abel 群）或交换群。

循环群：设 $\langle G, \ast \rangle$ 是群，若 $\exists \ g \in G, \forall a \in G, a = g ^ i(i \in \mathbb I)$，则称 $\langle G, \ast \rangle$ 为循环群。 $g$ 是循环群 $\langle G, \ast \rangle$ 的一个生成元。一个循环群的生成元个数可以不唯一。
与循环独异点不同的是，循环群中 $a = g ^ i$ 中的 $i$ 可以取负整数。在这里理解成对 $g$ 先求逆，再进行 $|i|$ 次的运算。

任何一个循环群必定是阿贝尔群。（证明：将元素写成生成元的幂的形式，再证明 $\ast$ 的可交换性，其中用到了加法是可交换的。）

6.7.5 循环群的性质

设 $\langle G, \ast \rangle$ 是循环群，它的生成元是 $g$，$n = |G|$，则：

1. $n$ 是使 $g ^ n = e$ 的最小正整数。

2. $G = { g ^ 1, g ^ 2, \cdots, g ^ n = e}$。

定理：循环群的子群必是循环群。

6.7.6 子群和群同态

设 $\langle G, \ast \rangle$ 是群， $S$ 是 $G$ 的非空子集。若：

1. $\forall a, b \in S, a \ast b \in S$ —— $\ast$ 在 $S$ 上封闭。

2. $\forall a \in S, a ^ {-1} \in S$ —— $S$ 中所有元素可逆。

3. $e \in S$， 其中 $e$ 是 $\langle G, \ast \rangle$ 的幺元 —— $S$ 包含和 $G$ 中一样的幺元。

则称 $\langle S, \ast \rangle$ 是 $\langle G, \ast \rangle$ 的子群。
$\langle G, \ast \rangle$ 和 $\langle { e}, \ast \rangle$ 称作 $\langle S, \ast \rangle$ 的平凡子群。（联想到子代数和平凡子代数的概念）

子群的判定1

设 $\langle G, \ast \rangle$ 是群， $S$ 是 $G$ 的非空子集。若运算 $\ast$ 在 $S$ 上封闭，并且 $\forall x \in S, x ^{-1} \in S$，则称 $\langle S, \ast \rangle$ 是 $\langle G, \ast \rangle$ 的子群。

子群的判定2

设 $\langle G, \ast \rangle$ 是群， $S$ 是 $G$ 的非空子集。若 $S$ 是有限集，并且 $\ast$ 在 $S$ 上封闭，则称 $\langle S, \ast \rangle$ 是 $\langle G, \ast \rangle$ 的子群。

子群的判定3

设 $\langle G, \ast \rangle$ 是群，$S$ 是 $G$ 的非空子集。若 $ \forall a, b \in S, a \ast b ^ {-1} \in S$，则称 $\langle S, \ast \rangle$ 是 $\langle G, \ast \rangle$ 的子群。

群同态

设 $\langle G, \ast \rangle$ 和 $\langle H, \circledast \rangle$ 是两个群， $h$ 是 $G$ 到 $H$ 的映射。若 $\forall a, b \in G$，都有 $h(a \ast b) = h(a) \circledast h(b)$，则称 $h$ 是 $\langle G, \ast \rangle$ 到 $\langle H, \circledast \rangle$ 的群同态，$\langle h(G), \circledast \rangle$ 称作 $\langle G, \ast \rangle$ 的同态象。（本质与之前的同态概念相同，先运算再映射 = 先映射再运算）

之前的同态是针对普通代数系统的，群同态的概念只是在代数系统是群的条件上产生的。

群同态的定理

群 $\langle G, \ast \rangle$ 的同态象 $\langle h(G), \circledast \rangle$ 是群 $\langle G, \ast \rangle$ 的子群。（证明：最朴素的子群证法）

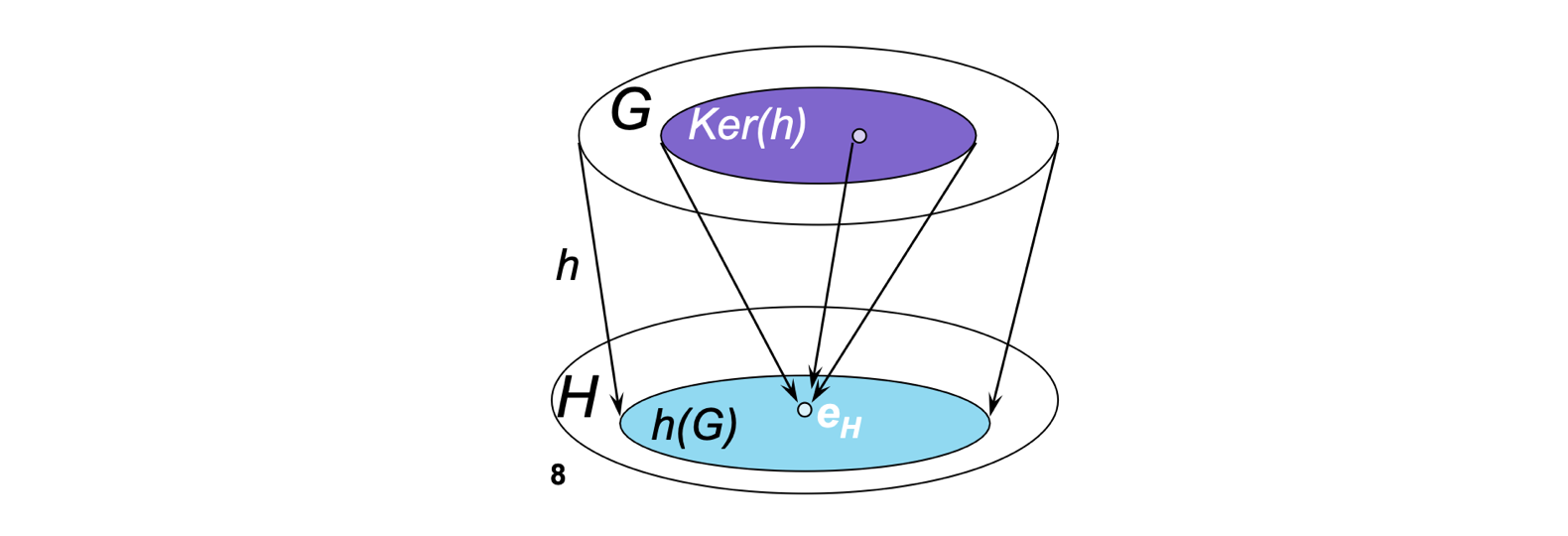
同态核

设 $h$ 是从群 $\langle G, \ast \rangle$ 到 $\langle H, \circledast \rangle$ 的一个同态映射， $e_H$ 是 $\langle H, \circledast \rangle$ 中的幺元。
定义：

$$
Ker(h) = { x | x \in G \wedge h(x) = e_{H}}
$$

称 $Ker(h)$ 为群同态映射 $h$ 的核，简称 $h$ 的同态核。

$\langle Ker(h), \ast \rangle$ 是 $\langle G, \ast \rangle$ 的子群。

循环群同态性质

设 $\langle G, \ast \rangle$ 是一个循环群，其生成元为 $g$ 。

1. 若 $|G|$ 是无限集，则 $\langle G, \ast \rangle$ 与 $\langle I, + \rangle$ 同构。

2. 若 $|G|$ 是有限集且其阶为 $k$, 则 $\langle G, \ast \rangle$ 与 $\langle N_k, +_{k} \rangle$ 同构。

6.7.7 陪集

设 $\langle H, \ast \rangle$ 是群 $\langle G, \ast \rangle$ 的一个子群。

左陪集：$a \in G$，集合 $aH = { a \ast b \ | \ b \in H}$，称为由 $a$ 确定的 $H$ 在 $G$ 中的左陪集。元素 $a \in aH$ 称为左陪集 $aH$ 的代表元素。

陪集的性质

1. 设 $\langle H, \ast \rangle$ 是群 $\langle G, \ast \rangle$ 的一个子群，$aH$ 和 $bH$ 是其任意两个左陪集。

• $aH = bH$ 或 $aH \bigcap bH = \phi $。

• $|aH| = |bH| = |H|$。

2. 设 $\langle H, \ast \rangle$ 是群 $\langle G, \ast \rangle$ 的一个子群，$a, b \in G$，$aH$ 是由 $a$ 确定的 $H$ 在 $G$ 中的左陪集。则 $b \in aH$ 当且仅当 $a ^ {-1} \ast b \in H$。

6.7.8 拉格朗日定理

设 $\langle H, \ast \rangle$ 是群 $\langle G, \ast \rangle$ 的一个子群，则：

• $R = { \langle a, b \rangle \ | \ a \in G \wedge b \in G \wedge a ^ {-1} \ast b \in H}$ 是 $G$ 中的等价关系，且有 $[a]_R = aH$。

• 若 $G$ 是有限群，$|G| = n$，$|H| = m$，则 $m \ | \ n$。

拉格朗日定理的推论

• 任何质数阶的群没有非平凡子群。

• 设 $\langle G, \ast \rangle$ 是 $n$ 阶有限群，则 $\forall a \in G$， $a$ 的阶数必定是 $n$ 的因子，且 $a ^ n = e$。

• 一个质数阶的群必定是循环群，且任何与幺元不同的元素均可作为生成元。

6.8 环和域

6.8.1 环

若代数系统 $\langle A, +, \cdot \rangle$ 满足：

• $\langle A, + \rangle$ 是阿贝尔群（$\langle A, + \rangle$ 是群且 $+$ 在 $A$ 上可交换）。

• $\langle A, \cdot \rangle$ 是半群（ $\cdot$ 在 $A$ 上可结合）。

• 乘法 $\cdot$ 和加法 $+$ 是可分配的。
  即 $\forall a, b, c \in A$，有：
  $$
  a \cdot (b + c) = a \cdot b + a \cdot c \ (b + c) \cdot a = b \cdot a + b \cdot c
  $$

则称 $\langle A, +, \cdot \rangle$ 是环。

环的定理

设 $\langle A, +, \cdot \rangle$ 是环，$\theta$ 是 $+$ 的幺元。则 $\forall a, b, c \in A$，有：

• $a \cdot \theta = \theta \cdot a = \theta$（$\theta$ 同时也是 $\cdot$ 的零元）

• $a \cdot (-b) = (-a) \cdot b = -a \cdot b$

• $(-a) \cdot (-b) = a \cdot b$

• $a \cdot (b - c) = a \cdot b - a \cdot c$

• $(b - c) \cdot a = b \cdot a - c \cdot a$

$-a$ 是 $a$ 的加法逆元，将 $a + (-b)$ 记作 $a - b$。

特殊的环

设 $\langle A, +, \cdot \rangle$ 是环:

• 交换环：若运算 $\cdot$ 是可交换的。

• 含幺环：若 $\langle A, \cdot \rangle$ 含有幺元。

• 含零因子环：$\theta$ 是 $+$ 的幺元，若 $\exists a, b \in A, a \neq \theta, b \neq \theta$，使得 $a \cdot b = \theta$，则称 $a, b$ 是零因子，称 $\langle A, +, \cdot \rangle$ 是含零因子环。

• 整环：$\langle A, \cdot \rangle$ 是可交换独异点且无零因子。

整环的定理

设 $\langle A, +, \cdot \rangle$ 是环，$\theta$ 是 $+$ 的幺元。$\langle A, +, \cdot \rangle$ 无零因子当且仅当 $\langle A, +, \cdot \rangle$ 满足可约律（即 $\forall a, b, c \in A, c \neq \theta$，若 $c \cdot a = c \cdot b$，必有 $a = b$）。

6.8.2 域

在代数系统 $\langle F, +, \cdot \rangle$ 中， $\theta$ 是 $+$ 的幺元，若：

• $\langle F, + \rangle$ 是阿贝尔群。

• $\langle F - { \theta }, \cdot \rangle$ 也是阿贝尔群。

• 乘法 $\cdot$ 和加法 $+$ 是可分配的。

则称 $\langle F, +, \cdot \rangle$ 是域。

域的定理

域一定是整环。可以通过整环的概念来定义域：
设 $\langle F, +, \cdot \rangle$ 是整环，$|F| > 1$，且 $\langle F - { \theta }, \cdot \rangle$ 是群，则 $\langle F, +, \cdot \rangle$ 是域。

有限整环一定是域。